If you recall in a recent Sunday Morning Insight: A Quick Panorama of Sensing from Direct Imaging to Machine Learning I pointed out that coded aperture imaging fell in the indirect imaging category with initially a linear encoder and linear decoder:
x = L(Ax)
But then with people like Zachary Harmany, Roummel Marcia, and Rebecca Willett, these systems could also be looked at as a compressive sensing ones with the following decomposition:
x = N(Ax) or even x = N(A(Bx))
with a linear encoder but a nonlinear decoder.
Here is the latest instance of their very interesting work in Compressive Coded Aperture Keyed Exposure Imaging with Optical Flow Reconstruction by Zachary Harmany, Roummel Marcia, and Rebecca Willet
This paper describes a coded aperture and keyed exposure approach to compressive video measurement which admits a small physical platform, high photon efficiency, high temporal resolution, and fast reconstruction algorithms. The proposed projections satisfy the Restricted Isometry Property (RIP), and hence compressed sensing theory provides theoretical guarantees on the video reconstruction quality. Moreover, the projections can be easily implemented using existing optical elements such as spatial light modulators (SLMs). We extend these coded mask designs to novel dual-scale masks (DSMs) which enable the recovery of a coarse-resolution estimate of the scene with negligible computational cost. We develop fast numerical algorithms which utilize both temporal correlations and optical flow in the video sequence as well as the innovative structure of the projections. Our numerical experiments demonstrate the efficacy of the proposed approach on short-wave infrared data.
I note the following tidbit:
In summary we see that the CAKE acquisitions are able to outperform traditionally sampled video in terms of reconstruction accuracy and reconstructing salient motion. On average, to reconstruct the 28 video frames, CAKE took 96 minutes and Dual-Scale Mask CAKE took 93 minutes, while CAKE with Optical Flow took only 31 minutes. Conventional spline upsampling took nearly 23 seconds
Emphasis is mine.
Ever since the beginning of compressive sensing, signal/image reconstruction has been Achille's heel of the technique. And as shown in this last paper, it is still an issue. This is very salient problem because it also means that any other technology developed with compressive sensing in mind, is likely to be a second class citizen to more direct, faster but less precise approaches. Like we say in Texas, it's a damn shame because compressive sensing allows new kinds of data acquisition (hyperspectral, 1-bit,...) with an attendant reduction in complexity on the hardware/sensor side. It's not just a question of nice sensors, it's an issue of direct economical impact. Who wouldn't want that ? These new fields will not develop or will remain a niche and expensive if the issue of data reconstruction is not solved. What's on the horizon ?
Let us first note that in the first few years, reconstruction speed increased dramatically allowing an order of magnitude speed gain per year for about three years.
This was nice, but the trend did not continue at that pace.
Let us turn our attention to different modalities that are currently being developed to see if there is a way we can leap forward in the future. All modalities I know seem to fall in the same broad category which follows some of the early thinking from neurosciences: build a neutral network with little if any feedback. ( see this 2007's entry on Compressed Sensing in the Primary Visual Cortex ?, Compressed Sensing, Primary Visual Cortex, Dimensionality Reduction, Manifolds and Autism )
Ever since the beginning of compressive sensing, signal/image reconstruction has been Achille's heel of the technique. And as shown in this last paper, it is still an issue. This is very salient problem because it also means that any other technology developed with compressive sensing in mind, is likely to be a second class citizen to more direct, faster but less precise approaches. Like we say in Texas, it's a damn shame because compressive sensing allows new kinds of data acquisition (hyperspectral, 1-bit,...) with an attendant reduction in complexity on the hardware/sensor side. It's not just a question of nice sensors, it's an issue of direct economical impact. Who wouldn't want that ? These new fields will not develop or will remain a niche and expensive if the issue of data reconstruction is not solved. What's on the horizon ?
Let us first note that in the first few years, reconstruction speed increased dramatically allowing an order of magnitude speed gain per year for about three years.
This was nice, but the trend did not continue at that pace.
Let us turn our attention to different modalities that are currently being developed to see if there is a way we can leap forward in the future. All modalities I know seem to fall in the same broad category which follows some of the early thinking from neurosciences: build a neutral network with little if any feedback. ( see this 2007's entry on Compressed Sensing in the Primary Visual Cortex ?, Compressed Sensing, Primary Visual Cortex, Dimensionality Reduction, Manifolds and Autism )
and I found three:
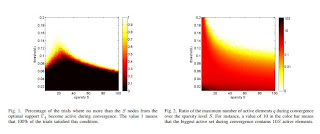
First, there is this approach by Aurele Balavoine, Chris Rozell, Justin Romberg [1,2] that builds up a analog neural network and study if it converges to the expected sparse solutions:
The Locally Competitive Algorithm (LCA) [8] is a continuous-time system of coupled nonlinear differential equations that settles to the minimizer of (1) in steady state [9]. The LCA architecture consists of simple components (matrixvector operations and a pointwise nonlinearity for thresholding), giving it the potential to be implemented in an analog circuit [10], [11]. Analog networks for solving optimization problems have a long history, dating back to Hopfield’s pioneering results for linear programming [12] (a comprehensive treatment of the subject can be found in [13]). Such analog systems can potentially have significant speed and power advantages over their digital counterparts.
and what do they find ?
that indeed few of neutral network branches were activated for sparse inputs! This is good,
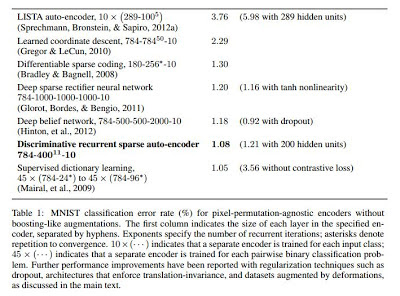
The second approach follows that of machine learning as applied in computer vision through the recent breakthrough in deep learning, i.e. the utilization of neutral networks with some unsupervised training algorithms to perform sparse coding. In the end and as mentioned in Sunday Morning Insight: A Quick Panorama of Sensing from Direct Imaging to Machine Learning. It comes down to the ability to build an encoder/decoder pair with a neutral network and using the right regularization to find some of the weights of the network. Examples of approaches mostly by the group of Yann LeCun can be found in [5,6,7,8,9]
From [7]
From [8]
From [8]
From [3]
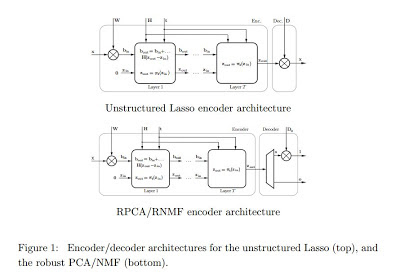
Finally, Pablo Sprechmann, Alex Bronstein, Guillermo Sapiro [3,4] made the case that a proximal approach could be implemented on learning encoder/decoder couples in order to produce an online sparse coding capability. It turns out that the iterative process can be truncated and directly mapped into a neutral network type of approach [5,6]
In their inspiring recent paper, [30] showed that a particular network architecture can be derived from the iterative shrinkage-thresholding (ISTA) [17] and proximal coordinate descent (CoD) algorithms [19].
That approach leads to very fast sparse coding and NMF decomposition type of results. As they point out in [3]
These works were among the first to bridge between the optimization based sparse models and the inherently process-centric neural networks, and in particular auto-encoder networks [31, 32], extensively explored by the deep learning community.
(please note the use of an iPad for the reconstruction task)
So roughly, all these solutions seem to converge toward a nonlinear reconstruction technique using neural networks or equivalent that have online training capabilities. I wonder how, instead of ISTA/FISTA, an AMP solution would provide an even faster capability since we know these iterations schemes to be pretty fast. It looks like the connection between neural networks and belief propagation is being made [10] (see also Blind Calibration in Compressed Sensing using Message Passing Algorithms )
Finally, I note that in most of these approaches based on computer vision, the dictionary learning phase uses the sparsity of the elements of the scene. In a compressive sensing scenario, the acquisition system captures an already compressed ( i.e. non sparse) version of the scene.
References:
Sparse approximation is an optimization program that produces state-of-the-art results in many applications in signal processing and engineering. To deploy this approach in real-time, it is necessary to develop faster solvers than are currently available in digital. The Locally Competitive Algorithm (LCA) is a dynamical system designed to solve the class of sparse approximation problems in continuous time. But before implementing this network in analog VLSI, it is essential to provide performance guarantees. This paper presents new results on the convergence of the LCA neural network. Using recently developed methods that make use of the Łojasiewicz inequality for nonsmooth functions, we prove that the output and state trajectories converge to a single fixed point. This improves on previous results by guaranteeing convergence to a singleton even when the optimization program has infinitely many and nonisolated solution points.
Abstract—This paper studies the convergence rate of a continuous-time dynamical system for `1-minimization, known as the Locally Competitive Algorithm (LCA). Solving `1-minimization problems efficiently and rapidly is of great interest to the signal processing community, as these programs have been shown to recover sparse solutions to underdetermined systems of linear equations and come with strong performance guarantees. The LCA under study differs from the typical `1-solver in that it operates in continuous time: instead of being specified by discrete iterations, it evolves according to a system of nonlinear ordinary differential equations. The LCA is constructed from simple components, giving it the potential to be implemented as a large-scale analog circuit. The goal of this paper is to give guarantees on the convergence time of the LCA system. To do so, we analyze how the LCA evolves as it is recovering a sparse signal from underdetermined measurements. We show that under appropriate conditions on the measurement matrix and the problem parameters, the path the LCA follows can be described as a sequence of linear differential equations, each with a small number of active variables. This allows us to relate the convergence time of the system to the restricted isometry constant of the matrix. Interesting parallels to sparse-recovery digital solvers emerge from this study. Our analysis covers both the noisy and noiseless settings and is supported by simulation results.
[3] Learning efficient sparse and low rank models by Pablo Sprechmann, Alex M. Bronstein, Guillermo Sapiro
Parsimony, including sparsity and low rank, has been shown to successfully model data in numerous machine learning and signal processing tasks. Traditionally, such modeling approaches rely on an iterative algorithm that minimizes an objective function with parsimony-promoting terms. The inherently sequential structure and data-dependent complexity and latency of iterative optimization constitute a major limitation in many applications requiring real-time performance or involving large-scale data. Another limitation encountered by these modeling techniques is the difficulty of their inclusion in discriminative learning scenarios. In this work, we propose to move the emphasis from the model to the pursuit algorithm, and develop a process-centric view of parsimonious modeling, in which a learned deterministic fixed-complexity pursuit process is used in lieu of iterative optimization. We show a principled way to construct learnable pursuit process architectures for structured sparse and robust low rank models, derived from the iteration of proximal descent algorithms. These architectures learn to approximate the exact parsimonious representation at a fraction of the complexity of the standard optimization methods. We also show that appropriate training regimes allow to naturally extend parsimonious models to discriminative settings. State-of-the-art results are demonstrated on several challenging problems in image and audio processing with several orders of magnitude speedup compared to the exact optimization algorithms.
In Sparse Coding (SC), input vectors are reconstructed using a sparse linear combination of basis vectors. SC has become a popular method for extracting features from data. For a given input, SC minimizes a quadratic reconstruction error with an L1 penalty term on the code. The process is often too slow for applications such as real-time pattern recognition. We proposed two versions of a very fast algorithm that produces approximate estimates of the sparse code that can be used to compute good visual features, or to initialize exact iterative algorithms. The main idea is to train a non-linear, feed-forward predictor with a specific architecture and a fixed depth to produce the best possible approximation of the sparse code. A version of the method, which can be seen as a trainable version of Li and Osher’s coordinate descent method, is shown to produce approximate solutions with 10 times less computation than Li and Osher’s for the same approximation error. Unlike previous proposals for sparse code predictors, the system allows a kind of approximate “explaining away” to take place during inference. The resulting predictor is differentiable and can be included into globally trained recognition systems.
[6] Fast Approximations to Structured Sparse Coding and Applications to Object Classification Arthur Szlam, Karol Gregor and Yann LeCun
We describe a method for fast approximation of sparse coding. A given input vector is passed through a binary tree. Each leaf of the tree contains a subset of dictionary elements. The coefficients corresponding to these dictionary elements are allowed to be nonzero and their values are calculated quickly by multiplication with a precomputed pseudoinverse. The tree parameters, the dictionary, and the subsets of the dictionary corresponding to each leaf are learned.In the process of describing this algorithm, we discuss the more general problem of learning the groups in group structured sparse modeling. We show that our method creates good sparse representations by using it in the object recognition framework of [1,2]. Implementing our own fast version of the SIFT descriptor the whole system runs at 20 frames per second on 321 × 481 sized images on alaptop with a quad-core cpu, while sacrificing very little accuracy on the Caltech101, Caltech 256, and 15 scenes benchmarks.[7] Li Wan, Matthew Zeiler, Sixin Zhang, Yann LeCun and Rob Fergus: Regularization of Neural Networks using DropConnect. DropConnect CUDA Code and page is here.
We introduce DropConnect, a generalization of Dropout (Hinton et al., 2012), for regularizing large fully-connected layers within neural networks. When training with Dropout, a randomly selected subset of activations are set to zero within each layer. DropConnect instead sets a randomly selected subset of weights within the network to zero. Each unit thus receives input from a random subset of units in the previous layer. We derive a bound on the generalization performance of both Dropout and DropConnect. We then evaluate DropConnect on a range of datasets, comparing to Dropout, and show state-of-the-art results on several image recognition benchmarks by aggregating multiple DropConnect-trained models.
We present the discriminative recurrent sparse auto-encoder model, comprising a recurrent encoder of rectified linear units, unrolled for a fixed number of iterations, and connected to two linear decoders that reconstruct the input and predict its supervised classification. Training via backpropagation-through-time initially minimizes an unsupervised sparse reconstruction error; the loss function is then augmented with a discriminative term on the supervised classification. The depth implicit in the temporally-unrolled form allows the system to exhibit far more representational power, while keeping the number of trainable parameters fixed. From an initially unstructured network the hidden units differentiate into categorical-units, each of which represents an input prototype with a well-defined class; and part-units representing deformations of these prototypes. The learned organization of the recurrent encoder is hierarchical: part-units are driven directly by the input, whereas the activity of categorical-units builds up over time through interactions with the part-units. Even using a small number of hidden units per layer, discriminative recurrent sparse auto-encoders achieve excellent performance on MNIST.
[9] Rotislav Goroshin and Yann LeCun: Saturating Auto-Encoders.
We introduce a simple new regularizer for auto-encoders whose hidden-unit activation functions contain at least one zero-gradient (saturated) region. This regularizer explicitly encourages activations in the saturated region(s) of the corresponding activation function. We call these Saturating Auto-Encoders (SATAE). We show that the saturation regularizer explicitly limits the SATAE’s ability to reconstruct inputs which are not near the data manifold. Furthermore, we show that a wide variety of features can be learned when different activation functions are used. Finally, connections are established with the Contractive and Sparse Auto-Encoders.[10] Intrinsic Gradient Networks, Jason Tyler Rolfe
Artificial neural networks are computationally powerful and exhibit brain-like dynamics. Unfortunately, the conventional gradient-dependent learning algorithms used to train them are biologically implausible. The calculation of the gradient in a traditional artificial neural network requires a complementary network of fast training signals that are dependent upon, but must not affect, the primary output-generating network activity. In contrast, the network of neurons in the cortex is highly recurrent; a network of gradient-calculating neurons in the brain would certainly project back to and influence the primary network. We address this biological implausibility by introducing a novel class of recurrent neural networks, intrinsic gradient networks, for which the gradient of an error function with respect to the parameters is a simple function of the network state. These networks can be trained using only their intrinsic signals, much like the network of neurons in the brain.We derive a simple equation that characterizes intrinsic gradient networks, and construct a broad set of networks that satisfy this characteristic equation. The resulting set of intrinsic gradient networks includes many highly recurrent instances for which the gradient can be calculated by a simple, local, pseudo-Hebbian function of the network state, thus resolving a long-standing contradiction between artificial and biological neural networks. We demonstrate that these networks can learn to perform nontrivial tasks like handwritten digit recognition using only their intrinsic signals. Finally, we show that a cortical implementation of an intrinsic gradient network would have a number of characteristic computational, anatomical, and electrophysiological properties, and review experimentalevidence suggesting the manifestation of these properties in the cortex.







2 comments:
Excellent post; you crystallized some of my own thoughts on this topic. Let me add a few other relevant thoughts.
You wrote "I wonder how, instead of ISTA/FISTA, an AMP solution would provide an even faster capability since we know these iterations schemes to be pretty fast."
My experience with sparse coders like ISTA/FISTA is that a warm start (i.e., a good guess of the solution) will reduce the number of needed iterations, hence speed up the sparse coding. When I read your [5], my thought was that the neural net did just that - provide a good guess and reducing the number of iterations by an order of magnitude.
Although I don't have direct experience with AMP, my understanding of the AMP literature is that few iterations are required. Hence I was thinking that in this case the neural net would not provide much speed improvement. But I could be wrong about this and would like to hear from an "AMP practitioner" as to the impact of a neural net or other good solution estimator on AMP.
Thanks again for this blog posting on this interesting topic.
Thanks Leslie.
Igor.
Post a Comment