The phase response curve (PRC), relating the phase shift of an oscillator to external perturbation, is an important tool to study neurons and their population behavior. It can be experimentally estimated by measuring the phase changes caused by probe stimuli. These stimuli, usually short pulses or continuous noise, have a much wider frequency spectrum than that of neuronal dynamics. This makes the experimental data high dimensional while the number of data samples tends to be small. Current PRC estimation methods have not been optimized for efficiently discovering the relevant degrees of freedom from such data. We propose a systematic and efficient approach based on a recently developed signal processing theory called Compressive Sensing (CS). CS is a framework for recovering sparsely constructed signals from undersampled data and is suitable for extracting information about the PRC from finite but high dimensional experimental measure- ments. We illustrate how the CS algorithm can be translated into an estimation scheme, and demonstrate that our CS method can produce good estimates of the PRCs with simulated and experimental data, especially when the data size is so small that simple approaches such as naive averaging fail. The tradeoffs between degrees of freedom versus goodness-of-fit were systematically analyzed, which help us to understand better what part of the data has the most predictive power. Our results illustrate that finite sizes of neuroscientific data in general compounded by large dimensionality can hamper studies of the neural code, and suggest that CS is a good tool for overcoming this challenge.
In recent work, two different methods have been used to characterize the fundamental limits of compressed sensing. On the one hand are rigorous bounds based on information theoretic arguments or the analysis of specific algorithms. On the other hand are exact but heuristic predictions made using the replica method from statistical physics. In this paper, it is shown that, for certain problem settings, these bounds are in agreement, and thus provide a rigorous and accurate characterization of the compressed sensing problem. This characterization shows that the limits of sparse recovery can be quantified succinctly in terms of an effective signal-to-interference-plus-noise ratio, that depends on the number of measurements and the behavior of the sparse components themselves. Connections with the MMSE dimension by Wu and Verdu and minimax behavior of approximate message passing by Donoho et al. are discussed.
The recently proposed Sparse Shape Composition (SSC) opens a new avenue for shape prior modeling. Instead of assuming any parametric model of shape statistics, SSC incorporates shape priors on-the-fly by approximating a shape instance (usually derived from appearance cues) by a sparse combination of shapes in a training repository. Theoretically, one can increase the modeling capability of SSC by including as many training shapes in the repository. However, this strategy confronts two limitations in practice. First, since SSC involves an iterative sparse optimization at run-time, the more shape instances contained in the repository, the less run-time efficiency SSC has. Therefore, a compact and informative shape dictionary is preferred to a large shape repository. Second, in medical imaging applications, training shapes seldom come in one batch. It is very time consuming and sometimes infeasible to reconstruct the shape dictionary every time new training shapes appear. In this paper, we propose an online learning method to address these two limitations. Our method starts from constructing an initial shape dictionary using the K-SVD algorithm. When new training shapes come, instead of re-constructing the dictionary from the ground up, we update the existing one using a block-coordinates descent approach. Using the dynamically updated dictionary, sparse shape composition can be gracefully scaled up to model shape priors from a large number of training shapes without sacrificing run-time efficiency. Our method is validated on lung localization in X-Ray and cardiac segmentation in MRI time series. Compared to the original SSC, it shows comparable performance while being significantly more efficient.
Nested Dictionary Learning for Hierarchical Organization of Imagery and Text by Lingbo Li, XianXing Zhang, Mingyuan Zhou, Lawrence Carin. The abstract: reads:
A tree-based dictionary learning model is developed for joint analysis of imagery and associated text. The dictionary learning may be applied directly to the imagery from patches, or to general feature vectors extracted from patches or superpixels (using any existing method for image feature extraction). Each image is associated with a path through the tree (from root to a leaf ), and each of the multiple patches in a given image is associated with one node in that path. Nodes near the tree root are shared between multiple paths, representing image characteristics that are common among di erent types ofimages. Moving toward the leaves, nodes become specialized, representing details in image classes. If available, words (text) are also jointly modeled, with a path-dependent probability over words. The tree structure is inferred via a nested Dirichlet process, and a retrospective stick-breaking sampler is used to infer the tree depth and width.
(Submitted on 18 Jun 2012)
We present a comprehensive framework for structured sparse coding and modeling extending the recent ideas of using learnable fast regressors to approximate exact sparse codes. For this purpose, we develop a novel block-coordinate proximal splitting method for the iterative solution of hierarchical sparse coding problems, and show an efficient feed forward architecture derived from its iteration. This architecture faithfully approximates the exact structured sparse codes with a fraction of the complexity of the standard optimization methods. We also show that by using different training objective functions, learnable sparse encoders are no longer restricted to be mere approximants of the exact sparse code for a pre-given dictionary, as in earlier formulations, but can be rather used as full-featured sparse encoders or even modelers. A simple implementation shows several orders of magnitude speedup compared to the state-of-the-art at minimal performance degradation, making the proposed framework suitable for real time and large-scale applications.
Demodulating Subsampled Direct Sequence Spread Spectrum Signals using Compressive Signal Processing
Karsten Fyhn,
Thomas Arildsen,
Torben Larsen,
Søren Holdt Jensen
(Submitted on 24 Oct 2011 (
v1), last revised 25 Jun 2012 (this version, v3))
We show that to lower the sampling rate in a spread spectrum communication system using Direct Sequence Spread Spectrum (DSSS), compressive signal processing can be applied to demodulate the received signal. This may lead to a decrease in the power consumption or the manufacturing price of wireless receivers using spread spectrum technology. The main novelty of this paper is the discovery that in spread spectrum systems it is possible to apply compressive sensing with a much simpler hardware architecture than in other systems, making the implementation both simpler and more energy efficient. Our theoretical work is exemplified with a numerical experiment using the IEEE 802.15.4 standard's 2.4 GHz band specification. The numerical results support our theoretical findings and indicate that compressive sensing may be used successfully in spread spectrum communication systems. The results obtained here may also be applicable in other spread spectrum technologies, such as Code Division Multiple Access (CDMA) systems.
Designing Incoherent Dictionaries for Compressed Sensing: Algorithm Comparison
Eliyahu Osherovich
(Submitted on 19 Jun 2012)
A new method presented for design of incoherent dictionaries.
Joint Reconstruction of Multi-view Compressed Images
Vijayaraghavan Thirumalai,
Pascal Frossard
(Submitted on 19 Jun 2012)
The distributed representation of correlated multi-view images is an important problem that arise in vision sensor networks. This paper concentrates on the joint reconstruction problem where the distributively compressed correlated images are jointly decoded in order to improve the reconstruction quality of all the compressed images. We consider a scenario where the images captured at different viewpoints are encoded independently using common coding solutions (e.g., JPEG, H.264 intra) with a balanced rate distribution among different cameras. A central decoder first estimates the underlying correlation model from the independently compressed images which will be used for the joint signal recovery. The joint reconstruction is then cast as a constrained convex optimization problem that reconstructs total-variation (TV) smooth images that comply with the estimated correlation model. At the same time, we add constraints that force the reconstructed images to be consistent with their compressed versions. We show by experiments that the proposed joint reconstruction scheme outperforms independent reconstruction in terms of image quality, for a given target bit rate. In addition, the decoding performance of our proposed algorithm compares advantageously to state-of-the-art distributed coding schemes based on disparity learning and on the DISCOVER.
A Hybrid Algorithm for Convex Semidefinite Optimization
Soeren Laue (Friedrich-Schiller-University)
(Submitted on 18 Jun 2012)
We present a hybrid algorithm for optimizing a convex, smooth function over the cone of positive semidefinite matrices. Our algorithm converges to the global optimal solution and can be used to solve general large-scale semidefinite programs and hence can be readily applied to a variety of machine learning problems. We show experimental results on three machine learning problems (matrix completion, metric learning, and sparse PCA) . Our approach outperforms state-of-the-art algorithms.
Invertibility of random matrices: unitary and orthogonal perturbations
Mark Rudelson,
Roman Vershynin
(Submitted on 22 Jun 2012)
We show that a perturbation of any fixed square matrix D by a random unitary matrix is well invertible with high probability. A similar result holds for perturbations by random orthogonal matrices; the only notable exception is when D is close to orthogonal. As an application, these results completely eliminate a hard-to-check condition from the Single Ring Theorem by Guionnet, Krishnapur and Zeitouni.
On multi-view feature learning
Roland Memisevic (University of Frankfurt)
(Submitted on 18 Jun 2012)
Sparse coding is a common approach to learning local features for object recognition. Recently, there has been an increasing interest in learning features from spatio-temporal, binocular, or other multi-observation data, where the goal is to encode the relationship between images rather than the content of a single image. We provide an analysis of multi-view feature learning, which shows that hidden variables encode transformations by detecting rotation angles in the eigenspaces shared among multiple image warps. Our analysis helps explain recent experimental results showing that transformation-specific features emerge when training complex cell models on videos. Our analysis also shows that transformation-invariant features can emerge as a by-product of learning representations of transformations.
Stability of matrix factorization for collaborative filtering
Yu-Xiang Wang (National University of Singapore),
Huan Xu (National University of Singapore)
(Submitted on 18 Jun 2012)
We study the stability vis a vis adversarial noise of matrix factorization algorithm for matrix completion. In particular, our results include: (I) we bound the gap between the solution matrix of the factorization method and the ground truth in terms of root mean square error; (II) we treat the matrix factorization as a subspace fitting problem and analyze the difference between the solution subspace and the ground truth; (III) we analyze the prediction error of individual users based on the subspace stability. We apply these results to the problem of collaborative filtering under manipulator attack, which leads to useful insights and guidelines for collaborative filtering system design.
Learning Efficient Structured Sparse Models
Alex Bronstein (Tel Aviv University),
Pablo Sprechmann (University of Minnesota),
Guillermo Sapiro(University of Minnesota)
(Submitted on 18 Jun 2012)
We present a comprehensive framework for structured sparse coding and modeling extending the recent ideas of using learnable fast regressors to approximate exact sparse codes. For this purpose, we develop a novel block-coordinate proximal splitting method for the iterative solution of hierarchical sparse coding problems, and show an efficient feed forward architecture derived from its iteration. This architecture faithfully approximates the exact structured sparse codes with a fraction of the complexity of the standard optimization methods. We also show that by using different training objective functions, learnable sparse encoders are no longer restricted to be mere approximants of the exact sparse code for a pre-given dictionary, as in earlier formulations, but can be rather used as full-featured sparse encoders or even modelers. A simple implementation shows several orders of magnitude speedup compared to the state-of-the-art at minimal performance degradation, making the proposed framework suitable for real time and large-scale applications.
Shift-Invariance Sparse Coding for Audio Classification
Roger Grosse,
Rajat Raina,
Helen Kwong,
Andrew Y. Ng
(Submitted on 20 Jun 2012)
Sparse coding is an unsupervised learning algorithm that learns a succinct high-level representation of the inputs given only unlabeled data; it represents each input as a sparse linear combination of a set of basis functions. Originally applied to modeling the human visual cortex, sparse coding has also been shown to be useful for self-taught learning, in which the goal is to solve a supervised classification task given access to additional unlabeled data drawn from different classes than that in the supervised learning problem. Shift-invariant sparse coding (SISC) is an extension of sparse coding which reconstructs a (usually time-series) input using all of the basis functions in all possible shifts. In this paper, we present an efficient algorithm for learning SISC bases. Our method is based on iteratively solving two large convex optimization problems: The first, which computes the linear coefficients, is an L1-regularized linear least squares problem with potentially hundreds of thousands of variables. Existing methods typically use a heuristic to select a small subset of the variables to optimize, but we present a way to efficiently compute the exact solution. The second, which solves for bases, is a constrained linear least squares problem. By optimizing over complex-valued variables in the Fourier domain, we reduce the coupling between the different variables, allowing the problem to be solved efficiently. We show that SISC's learned high-level representations of speech and music provide useful features for classification tasks within those domains. When applied to classification, under certain conditions the learned features outperform state of the art spectral and cepstral features.
Batched Sparse Codes
Shenghao Yang,
Raymond W. Yeung
(Submitted on 23 Jun 2012)
BATched Sparse codes (BATS codes) are proposed for transmitting a collection of packets through a communication network with packet loss. A BATS code consists of an inner code and an outer code over a finite field. The outer code is a matrix generalization of a fountain code that preserves desirable properties of the latter such as ratelessness and low encoding/decoding complexity. The outer code encodes the file to be transmitted into batches, each of which containing M packets. When the batch size M is equal to 1, the outer code reduces to a fountain code. The inner code is comprised of the linear network coding performed by the intermediate network nodes. With the constraint that linear network coding is applied only to packets within the same batch, the structure of the outer code is preserved. Furthermore, the computational capability of the intermediate network nodes required to apply BATS codes is independent of the number of packets for transmission. For tree networks, the size of the buffer required at the intermediate nodes is also independent of the number of packets for transmission. It is verified theoretically for certain cases and demonstrated numerically for some general cases that BATS codes asymptotically achieve rates very close to the capacity of the underlying networks.
On Deterministic Sketching and Streaming for Sparse Recovery and Norm Estimation
Jelani Nelson,
Huy Nguyen,
David P. Woodruff
(Submitted on 25 Jun 2012)
We study classic streaming and sparse recovery problems using deterministic linear sketches, including l1/l1 and linf/l1 sparse recovery problems (the latter also being known as l1-heavy hitters), norm estimation, and approximate inner product. We focus on devising a fixed matrix A in R^{m x n} and a deterministic recovery/estimation procedure which work for all possible input vectors simultaneously. Our results improve upon existing work, the following being our main contributions:
* A proof that linf/l1 sparse recovery and inner product estimation are equivalent, and that incoherent matrices can be used to solve both problems. Our upper bound for the number of measurements is m=O(eps^{-2}*min{log n, (log n / log(1/eps))^2}). We can also obtain fast sketching and recovery algorithms by making use of the Fast Johnson-Lindenstrauss transform. Both our running times and number of measurements improve upon previous work. We can also obtain better error guarantees than previous work in terms of a smaller tail of the input vector.
* A new lower bound for the number of linear measurements required to solve l1/l1 sparse recovery. We show Omega(k/eps^2 + klog(n/k)/eps) measurements are required to recover an x' with |x - x'|_1 <= (1+eps)|x_{tail(k)}|_1, where x_{tail(k)} is x projected onto all but its largest k coordinates in magnitude.
* A tight bound of m = Theta(eps^{-2}log(eps^2 n)) on the number of measurements required to solve deterministic norm estimation, i.e., to recover |x|_2 +/- eps|x|_1.
For all the problems we study, tight bounds are already known for the randomized complexity from previous work, except in the case of l1/l1 sparse recovery, where a nearly tight bound is known. Our work thus aims to study the deterministic complexities of these problems.
Joel Andersson,
Jan-Olov Strömberg
(Submitted on 26 Jun 2012)
This paper considers some new and some previously known results from the theory of compressive sensing. In particular a theorem concerning uniform recovery of structured random matrices by Rauhut et. al. We present an improved version of this theorem with a shorter proof. Furthermore we strengthen a result by Foucart et. al. regarding when the so called Restricted Isometry Property implies the Null Space Property for a matrix.
Stabilizing Nonuniformly Quantized Compressed Sensing with Scalar Companders
L. Jacques,
D. K. Hammond,
M. J. Fadili
(Submitted on 26 Jun 2012)
This paper studies the problem of reconstructing sparse or compressible signals from compressed sensing measurements that have undergone nonuniform quantization. Previous approaches to this Quantized Compressed Sensing (QCS) problem based on Gaussian models (bounded l2-norm) for the quantization distortion yield results that, while often acceptable, may not be fully consistent: re-measurement and quantization of the reconstructed signal do not necessarily match the initial observations. Quantization distortion instead more closely resembles heteroscedastic uniform noise, with variance depending on the observed quantization bin. Generalizing our previous work on uniform quantization, we show that for nonuniform quantizers described by the "compander" formalism, quantization distortion may be better characterized as having bounded weighted lp-norm (p >= 2), for a particular weighting. We develop a new reconstruction approach, termed Generalized Basis Pursuit DeNoise (GBPDN), which minimizes the sparsity of the reconstructed signal under this weighted lp-norm fidelity constraint. We prove that for B bits per measurement and under the oversampled QCS scenario (when the number of measurements is large compared to the signal sparsity) if the sensing matrix satisfies a proposed generalized Restricted Isometry Property, then, GBPDN provides a reconstruction error of sparse signals which decreases like O(2^{-B}/\sqrt{p+1}): a reduction by a factor \sqrt{p+1} relative to that produced by using the l2-norm. Besides the QCS scenario, we also show that GBPDN applies straightforwardly to the related case of CS measurements corrupted by heteroscedastic Generalized Gaussian noise with provable reconstruction error reduction. Finally, we describe an efficient numerical procedure for computing GBPDN via a primal-dual convex optimization scheme, and demonstrate its effectiveness through simulations.
The following paper feature some material that can be used to modulate a signal as is done in compressive sensing:
Liquid Crystal Tunable Metamaterial Perfect Absorber
David Shrekenhamer,
Wen-Chen Chen,
Willie J. Padilla
(Submitted on 19 Jun 2012)
We present experimental demonstration of electronically tunable metamaterial perfect absorbers in the terahertz regime. By incorporation of active liquid crystal into strategic locations within the metamaterial unit cell we are able to modify the absorption by 30 percent at 2.62 THz, as well as tune the resonant absorption over 4 percent in bandwidth. Numerical full-wave simulations match well to experiments and clarify the underlying mechanism, i.e. a simultaneous tuning of both the electric and magnetic response that allows for the preservation of the resonant absorption. These results show that the fundamental light interactions of surfaces can be dynamically controlled by all-electronic means and provide a path forward for realization of novel applications.
Is margin preserved after random projection?
Qinfeng Shi (The University of Adelaide),
Chunhua Shen (The University of Adelaide),
Rhys Hill (The University of Adelaide),
Anton van den Hengel (the University of Adelaide)
(Submitted on 18 Jun 2012)
Random projections have been applied in many machine learning algorithms. However, whether margin is preserved after random projection is non-trivial and not well studied. In this paper we analyse margin distortion after random projection, and give the conditions of margin preservation for binary classification problems. We also extend our analysis to margin for multiclass problems, and provide theoretical bounds on multiclass margin on the projected data.
Rank-based model selection for multiple ions quantum tomography
Madalin Guta,
Theodore Kypraios,
Ian Dryden
(Submitted on 18 Jun 2012)
The statistical analysis of measurement data has become a key component of many quantum engineering experiments. As standard full state tomography becomes unfeasible for large dimensional quantum systems, one needs to exploit prior information and the "sparsity" properties of the experimental state in order to reduce the dimensionality of the estimation problem. In this paper we propose model selection as a general principle for finding the simplest, or most parsimonious explanation of the data, by fitting different models and choosing the estimator with the best trade-off between likelihood fit and model complexity. We apply two well established model selection methods -- the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) -- to models consising of states of fixed rank and datasets such as are currently produced in multiple ions experiments. We test the performance of AIC and BIC on randomly chosen low rank states of 4 ions, and study the dependence of the selected rank with the number of measurement repetitions for one ion states. We then apply the methods to real data from a 4 ions experiment aimed at creating a Smolin state of rank 4. The two methods indicate that the optimal model for describing the data lies between ranks 6 and 9, and the Pearson $\chi^{2}$ test is applied to validate this conclusion. Additionally we find that the mean square error of the maximum likelihood estimator for pure states is close to that of the optimal over all possible measurements.
Collaborative Topic Regression with Social Matrix Factorization for Recommendation Systems
Sanjay Purushotham (Univ. of Southern California),
Yan Liu (Univ. of Southern California),
C.-C. Jay Kuo(Univ. of Southern California)
(Submitted on 18 Jun 2012)
Social network websites, such as Facebook, YouTube, Lastfm etc, have become a popular platform for users to connect with each other and share content or opinions. They provide rich information for us to study the influence of user's social circle in their decision process. In this paper, we are interested in examining the effectiveness of social network information to predict the user's ratings of items. We propose a novel hierarchical Bayesian model which jointly incorporates topic modeling and probabilistic matrix factorization of social networks. A major advantage of our model is to automatically infer useful latent topics and social information as well as their importance to collaborative filtering from the training data. Empirical experiments on two large-scale datasets show that our algorithm provides a more effective recommendation system than the state-of-the art approaches. Our results reveal interesting insight that the social circles have more influence on people's decisions about the usefulness of information (e.g., bookmarking preference on Delicious) than personal taste (e.g., music preference on Lastfm). We also examine and discuss solutions on potential information leak in many recommendation systems that utilize social information.
Clustering by Low-Rank Doubly Stochastic Matrix Decomposition
Zhirong Yang (Aalto University),
Erkki Oja (Aalto University)
(Submitted on 18 Jun 2012)
Clustering analysis by nonnegative low-rank approximations has achieved remarkable progress in the past decade. However, most approximation approaches in this direction are still restricted to matrix factorization. We propose a new low-rank learning method to improve the clustering performance, which is beyond matrix factorization. The approximation is based on a two-step bipartite random walk through virtual cluster nodes, where the approximation is formed by only cluster assigning probabilities. Minimizing the approximation error measured by Kullback-Leibler divergence is equivalent to maximizing the likelihood of a discriminative model, which endows our method with a solid probabilistic interpretation. The optimization is implemented by a relaxed Majorization-Minimization algorithm that is advantageous in finding good local minima. Furthermore, we point out that the regularized algorithm with Dirichlet prior only serves as initialization. Experimental results show that the new method has strong performance in clustering purity for various datasets, especially for large-scale manifold data.
Stability of matrix factorization for collaborative filtering
Yu-Xiang Wang (National University of Singapore),
Huan Xu (National University of Singapore)
(Submitted on 18 Jun 2012)
We study the stability vis a vis adversarial noise of matrix factorization algorithm for matrix completion. In particular, our results include: (I) we bound the gap between the solution matrix of the factorization method and the ground truth in terms of root mean square error; (II) we treat the matrix factorization as a subspace fitting problem and analyze the difference between the solution subspace and the ground truth; (III) we analyze the prediction error of individual users based on the subspace stability. We apply these results to the problem of collaborative filtering under manipulator attack, which leads to useful insights and guidelines for collaborative filtering system design.
Robust PCA in High-dimension: A Deterministic Approach
Jiashi Feng (NUS),
Huan Xu (NUS),
Shuicheng Yan (NUS)
(Submitted on 18 Jun 2012)
We consider principal component analysis for contaminated data-set in the high dimensional regime, where the dimensionality of each observation is comparable or even more than the number of observations. We propose a deterministic high-dimensional robust PCA algorithm which inherits all theoretical properties of its randomized counterpart, i.e., it is tractable, robust to contaminated points, easily kernelizable, asymptotic consistent and achieves maximal robustness -- a breakdown point of 50%. More importantly, the proposed method exhibits significantly better computational efficiency, which makes it suitable for large-scale real applications.
Robust Multiple Manifolds Structure Learning
Dian Gong (Univ. of Southern California),
Xuemei Zhao (Univ of Southern California),
Gerard Medioni(University of Southern California)
(Submitted on 18 Jun 2012)
We present a robust multiple manifolds structure learning (RMMSL) scheme to robustly estimate data structures under the multiple low intrinsic dimensional manifolds assumption. In the local learning stage, RMMSL efficiently estimates local tangent space by weighted low-rank matrix factorization. In the global learning stage, we propose a robust manifold clustering method based on local structure learning results. The proposed clustering method is designed to get the flattest manifolds clusters by introducing a novel curved-level similarity function. Our approach is evaluated and compared to state-of-the-art methods on synthetic data, handwritten digit images, human motion capture data and motorbike videos. We demonstrate the effectiveness of the proposed approach, which yields higher clustering accuracy, and produces promising results for challenging tasks of human motion segmentation and motion flow learning from videos.
Kai Zhang (Siemens),
Liang Lan (temple university),
Jun Liu (Siemens),
andreas Rauber (TU Wien),
Fabian Moerchen (Siemens Corporate Research and Technology)
(Submitted on 18 Jun 2012)
Low-rank matrix decomposition has gained great popularity recently in scaling up kernel methods to large amounts of data. However, some limitations could prevent them from working effectively in certain domains. For example, many existing approaches are intrinsically unsupervised, which does not incorporate side information (e.g., class labels) to produce task specific decompositions; also, they typically work "transductively", i.e., the factorization does not generalize to new samples, so the complete factorization needs to be recomputed when new samples become available. To solve these problems, in this paper we propose an"inductive"-flavored method for low-rank kernel decomposition with priors. We achieve this by generalizing the Nystr\"om method in a novel way. On the one hand, our approach employs a highly flexible, nonparametric structure that allows us to generalize the low-rank factors to arbitrarily new samples; on the other hand, it has linear time and space complexities, which can be orders of magnitudes faster than existing approaches and renders great efficiency in learning a low-rank kernel decomposition. Empirical results demonstrate the efficacy and efficiency of the proposed method.
Information-theoretic Semi-supervised Metric Learning via Entropy Regularization
Gang Niu (Tokyo Institute of Technology),
Bo Dai (Purdue University),
Makoto Yamada (Tokyo Institute of Technology),
Masashi Sugiyama (Tokyo Institute of Technology)
(Submitted on 18 Jun 2012)
We propose a general information-theoretic approach called Seraph (SEmi-supervised metRic leArning Paradigm with Hyper-sparsity) for metric learning that does not rely upon the manifold assumption. Given the probability parameterized by a Mahalanobis distance, we maximize the entropy of that probability on labeled data and minimize it on unlabeled data following entropy regularization, which allows the supervised and unsupervised parts to be integrated in a natural and meaningful way. Furthermore, Seraph is regularized by encouraging a low-rank projection induced from the metric. The optimization of Seraph is solved efficiently and stably by an EM-like scheme with the analytical E-Step and convex M-Step. Experiments demonstrate that Seraph compares favorably with many well-known global and local metric learning methods.
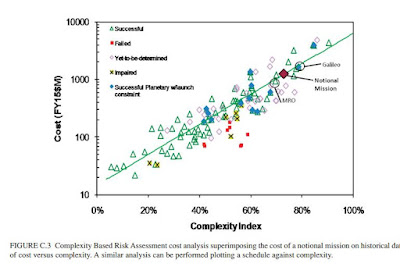
Image Credit: NASA/JPL-Caltech/Cornell/Arizona State Univ.
 Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from
Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also
subscribe to Nuit Blanche by Email, explore the
Big Picture in Compressive Sensing or the
Matrix Factorization Jungle and join the conversations on
compressive sensing,
advanced matrix factorization and
calibration issues on Linkedin.
.JPG)


.JPG)
.JPG)
