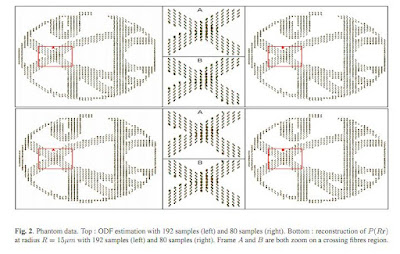
In diffusion magnetic resonance imaging (dMRI), the Ensemble Average Propagator (EAP), also known as the propagator, describes completely the water molecule diffusion in the brain white matter without any prior knowledge about the tissue shape. In this paper, we describe a new and efficient method to accurately reconstruct the EAP in terms of the Spherical Polar Fourier (SPF) basis from very few diffusion weighted magnetic resonance images (DW-MRI). This approach nicely exploits the duality between SPF and a closely related basis in which one can respectively represent the EAP and the diffusion signal using the same coefficients, and efficiently combines it to the recent acquisition and reconstruction technique called Compressed Sensing (CS). Our work provides an efficient analytical solution to estimate, from few measurements, the diffusion propagator at any radius. We also provide a new analytical solution to extract an important feature characterising the tissue microstructure: the Orientation Distribution Function (ODF). We illustrate and prove the effectiveness of our method in reconstructing the propagator and the ODF on both noisy multiple q-shell synthetic and phantom data.
and here is an abstract:
Predicting Catastrophes in Nonlinear Dynamical Systems by Compressive Sensing by Wen-Xu Wang, Rui Yang, Ying-Cheng Lai, Vassilios Kovanis, and Celso Grebogi. The abstract reads:
An extremely challenging problem of significant interest is to predict catastrophes in advance of their occurrences. We present a general approach to predicting catastrophes in nonlinear dynamical systems under the assumption that the system equations are completely unknown and only time series reflecting the evolution of the dynamical variables of the system are available. Our idea is to expand the vector field or map of the underlying system into a suitable function series and then to use the compressive-sensing technique to accurately estimate the various terms in the expansion. Examples using paradigmatic chaotic systems are provided to demonstrate our idea.
Finally, here is s
PhD studentship with Toshiba and University of Bristol:
DHPA PhD Vacancy Compressive Sensing
Industrial DHPA PhD Studentship Vacancy
An Industrial PhD Studentship funded by the ESPRC through the 2011 Dorothy Hodgkin Postgraduate Award Scheme (DHPA) is available in the Centre for Communications Research (CCR) at the University of Bristol in collaboration with Toshiba Research Europe Ltd (TREL).
The project is entitled “Compressive sensing for M2M applications including healthcare and smart energy”. Compressive sensing is the exploitation of certain characteristics of a signal such that less sampled data (less than Nyquist rate) can be used to reconstruct the signal. In the context of this proposal, compressive sensing is especially useful in reducing the required amount of sensor data to be acquired, such that these can be wirelessly transmitted at a low rate. As the data cannot be reconstructed in the normal way, it will also provide a means of protecting the privacy of the user. In this project, the student will look at ways of designing compressive sensing algorithm to exploit sparsity in M2M data such as biomedical signals or smart energy sensor data. However, the design will have to take special care such that irregularity in the signals which could be vital, will not be lost in the sensing process. Additionally, the student will look at algorithms to best reconstruct the compressed data.
In a nutshell, the project considers the following problems:
• Compressive sensing of M2M sensor data to achieve low rate sampling while capturing all vital irregularities in the signals,
• Design compressive sensing algorithms which are able to protect M2M sensor data from eavesdroppers or wireless sniffers,
• Optimising the reconstruction of compressed M2M data to remove noise and recover the original signal,
• Study implications of applying compressed sensing in a practical M2M environment such as healthcare and smart energy networks.
During the PhD programme, the student may undertake a placement at TREL’s Telecommunications Research Laboratory based in Bristol; while the student would benefit from the interactions with industrial researchers as well as the experience of working in an industrial laboratory, this is not mandated and is open to discussion.
This studentship is available from October 2011 for a period of up to 4 years and is funded jointly by the EPSRC through the 2011 Dorothy Hodgkin Postgraduate Award Scheme (DHPA) and by Toshiba Research Europe Ltd. The award provides an annual stipend ca. £13,590 per annum plus an enhancement of £1,430 per annum and full payment of Overseas Tuition Fees. Due to funding restrictions this studentship is only open to students from the countries listed at the OECD website - http://www.oecd.org/dataoecd/62/48/41655745.pdf - plus Russia and Hong Kong.
We are seeking students with equivalent of a UK first class honours degree, from a reputable academic institution. We welcome candidates who have strong backgrounds in one of the following areas: electronics and electrical engineering, computer science, applied mathematics, system control, or related disciplines
The project will be supervised by Dr. Rob Piechocki of CCR, and Drs Woon Hau Chin and Zhong Fan at Toshiba Research Europe Ltd. Further details of the CCR’s work are at: www.bristol.ac.uk/ccr.
Further details of the studentship can be found at:
http://www.rcuk.ac.uk/ResearchCareers/dhpa
Please e-mail your application to
http://www.bristol.ac.uk/prospectus/postgraduate/2011/intro/apply.html and use this same address if you have questions or would like to have an informal discussion about the post and the research project.
The start date is as soon as possible after the 1 October 2011 and no later than 1 October 2012. This studentship is open until filled.

















