Here is the reason we want phase transition curves as a means of providing insight: Clarity. We first had this stunning development in breaking the Donoho-Tanner phase transition which saw the possibility of getting optimal results with specially seeded matrices (and an AMP solver)[2]. Surprisingly and if I am not mistaken, all the other approaches require a block sparse signal assumption and specific solvers, There is the work with B-SBL and the more theoretically grounded work using Stein's shrinkage within an AMP solver [1] (which I cannot find an implementation for).
Today we have a study that takes the view that the signal is still block sparse but the authors try to figure out whether a group LASSO or a Stein's shrinkage/AMP combination provide better phase transition (see below).
[side note: By the way, if you want to know more about Message passing and approximate message passing, here is a presentation by Arian Maleki, ]
from a short summary
Maximin Analysis of Message Passing Algorithms for Recovering Block Sparse Signals by Armeen Taeb, Arian Maleki, Christoph Studer, Richard Baraniuk. The abstract reads:
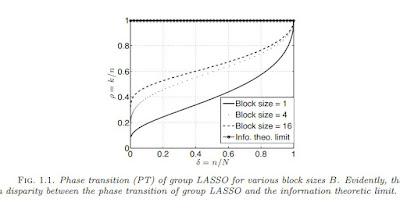
We consider the problem of recovering a block (or group) sparse signal from an underdetermined set of random linear measurements, which appear in compressed sensing applications such as radar and imaging. Recent results of Donoho, Johnstone, and Montanari have shown that approximate message passing (AMP) in combination with Stein's shrinkage outperforms group LASSO for large block sizes. In this paper, we prove that, for a fixed block size and in the strong undersampling regime (i.e., having very few measurements compared to the ambient dimension), AMP cannot improve upon group LASSO, thereby complementing the results of Donoho et al.
[1] D. L. Donoho, I. M. Johnstone, and A. Montanari. Accurate prediction of phase transitions incompressed sensing via a connection to minimax denoising. arXiv: 1108.0477, 2011.
[2] Probabilistic Reconstruction in Compressed Sensing: Algorithms, Phase Diagrams, and Threshold Achieving Matrices by Florent Krzakala, Marc Mézard,François Sausset, Yifan Sun, Lenka Zdeborová

No comments:
Post a Comment