In the following paper, I note four items of note beyond the very interesting results of the paper:
- an implementation of the paper is made available with the paper
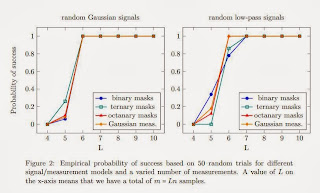
- the possibility of a sharp phase transition in phase retrieval (see figure below and mentioned in 2.3)
- Terry Tao mentioned it in the selected paper network, and you may recall the last words in this week's Sunday Morning Insight: The Map Makers that directed to Gilles Pisier's Grothendieck's theorem past and present
- Finally, the prominent use of two references [2] and [3] that are blog posts written by Dustin Mixon often featured in the Around the blogs in 78 hours. All the phase retrieval posts on Dustin's blog are at: http://dustingmixon.wordpress.com/category/phase-retrieval/
In addition, GT [Grothendieck's theorem] independently surfaced in several quite unrelated fi elds: ....in computer science where the Grothendieck inequality is invoked to replace certain NP hard problems by others that can be treated by 'semide finite programming' and hence solved in polynomial time.
This is an instance of an NP problem being replaced by semidefinite programming which in this paper is further relaxed into a convex programming problem.
Without further due, here is the paper:
Here is the paper: Phase Retrieval from masked Fourier transforms by Emmanuel Candes, Xiaodong Li, Mahdi Soltanolkotabi
This paper considers the question of recovering the phase of an object from intensity-only measurements, a problem which naturally appears in X-ray crystallography and related disciplines. We study a physically realistic setup where one can modulate the signal of interest and then collect the intensity of its diff raction pattern, each modulation thereby producing a sort of coded di ffraction pattern. We show that PhaseLift, a recent convex programming technique, recovers the phase information exactly from a number of random modulations, which is polylogarithmic in the number of unknowns. Numerical experiments with noiseless and noisy data complement our theoretical analysis and illustrate our approach.
The implementation is located here. Thanks Mahdi for the heads-ups.
3 comments:
FYI - More info on this paper can be found in an interview with Mahdi on my blog:
http://dustingmixon.wordpress.com/2013/11/13/phase-retrieval-from-coded-diffraction-patterns/
A sharp phase transition in phase retrieval was also shown in http://www2.ece.ohio-state.edu/~schniter/pdf/all12_phase.pdf
on a related topic:
http://forum.sci.ccny.cuny.edu/administration/mathematics/events/february-2014/mathematics-colloquium-hau-tieng-wu-stanford-university-alternating-projection-ptychography-and-high-dimensional-phase-retrieval
Post a Comment