Weiyu Xu just sent me the following:
"...We designed one SANDWICHING algorithm which can efficiently and precisely verify the well-known null space conditions in compressed sensing, which is famously known to hard. The feature of the algorithm is that it can find the EXACT value for the null space properties, with much reduced computational complexity than exhaustive search, for example, reducing a computational load of around 1 month (32) days to 4 hours. ...Best Regards,Xu,Weiyu"
This is very interesting! Thanks Weiyu !
Here is the paper: Precisely Verifying the Null Space Conditions in Compressed Sensing: A Sandwiching Algorithm by Myung Cho, Weiyu Xu
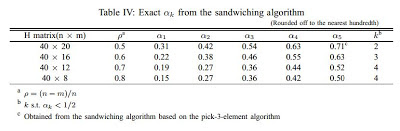
In this paper, we propose new efficient algorithms to verify the null space condition in compressed sensing (CS). Given an $(n-m) \times n$ ($m>0$) CS matrix $A$ and a positive $k$, we are interested in computing $\displaystyle \alpha_k = \max_{\{z: Az=0,z\neq 0\}}\max_{\{K: |K|\leq k\}}$ $\frac{\|z_K \|_{1}}{\|z\|_{1}}$, where $K$ represents subsets of $\{1,2,...,n\}$, and $|K|$ is the cardinality of $K$. In particular, we are interested in finding the maximum $k$ such that $\alpha_k < \frac{1}{2}$. However, computing $\alpha_k$ is known to be extremely challenging. In this paper, we first propose a series of new polynomial-time algorithms to compute upper bounds on $\alpha_k$. Based on these new polynomial-time algorithms, we further design a new sandwiching algorithm, to compute the \emph{exact} $\alpha_k$ with greatly reduced complexity. When needed, this new sandwiching algorithm also achieves a smooth tradeoff between computational complexity and result accuracy. Empirical results show the performance improvements of our algorithm over existing known methods; and our algorithm outputs precise values of $\alpha_k$, with much lower complexity than exhaustive search.
Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.
No comments:
Post a Comment