Hindsight is always 20/20: In X-ray CT, there is a full fledged and mature market for scanners with entire companies' bottom lines dependent on improving them. In that technology area, compressive sensing solvers are eventually formalizing the need to use the sparsity of the scene as a useful prior information. It also potentially helps the bottom line of the companies in that market.
If on the other hand, you create a new technology from scratch, you really don't have the luxury of specializing too early and therefore it is understandable that one would not want to rely on exotic solvers such as those in compressive sensing to deliver a viable product.
While convenient, algorithms such as Filtered Back Projection (FBP), traditional Inverse FFT with missing values or the current techniques used in Hartmanngram deconvolution rely on unstated assumptions that may not be relevant to the imaged scene thus leading to potentially sub-optimal imagery products. Here are two examples I chose from a recent meeting that can be found in many other areas of sensor design.
If on the other hand, you create a new technology from scratch, you really don't have the luxury of specializing too early and therefore it is understandable that one would not want to rely on exotic solvers such as those in compressive sensing to deliver a viable product.
But this is also a bad bet.
While convenient, algorithms such as Filtered Back Projection (FBP), traditional Inverse FFT with missing values or the current techniques used in Hartmanngram deconvolution rely on unstated assumptions that may not be relevant to the imaged scene thus leading to potentially sub-optimal imagery products. Here are two examples I chose from a recent meeting that can be found in many other areas of sensor design.
Back in March, I attended (and very much enjoyed!) the 7th meeting on unconventional optical imaging systems ( 7ème édition des journees « Imagerie Optique Non Conventionnelle ») hosted at ESPCI where many different hardware and sensors instances were being featured. While listening to the talks, I paid a specific attention to how sensors were designed with the sparsity of the scene in mind (either in the canonical basis or some other basis to be learned later). Few did in what I would characterize as a faulty sense of convenience.
From the standpoint of the sensor designer, one wants to generally shy away from the specifics of the object or the scene being imaged. Indeed, if a new sensor becomes too specific, it runs the real risk of being irrelevant overall. However, in light of the development in compressive sensing, designers ought to consider that numerical techniques currently used to reconstruct images are themselves built on some unstated and not necessarily relevant prior assumptions. Compressive sensing allows one to acknowledge that prior information and sometimes deal with it.
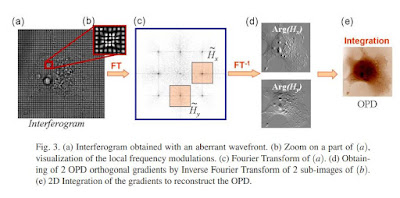
In the presentation entitled «Reconstruction 3D, sur un microscope standard, d’un échantillon biologique par tomographie diffractive en illumination spatialement incohérente» by Pierre Bon, Julien Savatier, Benoit Wattellier, Serge Monneret, the presenter showed a 3D extension of a 2009 paper [1} featuring Quadriwave lateral shearing interferometry.
What was striking there was how the artifacts of the reconstruction (right hand side of the figure shown above) looked eerlily similar to those FFT artifacts generally produced by the FBP used in CT. In the presentation, one could see that the reconstruction (top right figure in the figure below) had to be additionally filtered to extract a "good" image out of it (bottom right figure in the figure below). What sort of additional constraints were involved in this filtering, nobody knows.
While convenient, the current technique used in this Hartmanngram deconvolution rely on some unstated assumptions that may not be relevant to the scene being imaged yielding potentially suboptimal imagery.
If one pays a more particular attention to the imaging scene, it seems clear that microscopy of living cells is bound to feature mostly interfaces yielding images with sparse gradients as their main features. With that information in mind, one could possibly use quadriwave lateral shearing interferometry to reconstruct these sparse gradient scenes through solvers developed in compressive sensing.
In another presentation entitled « Microscopie tomographique diffractive en transmission et réflexion » by H. Liu, J. Bailleul, B. Simon, M. Debailleul, O. Haeberlé (see also [3] High resolution reflection tomographic diffractive microscopy) . The experimental set-up used two arms in order to have access to two sections of the Fourier plane. From what I understood, people generally use one arm or the other but not both at the same time.
Again having access to more of the Fourier space is a good thing. However if, as shown in the figure above, it does not improve tremendously a simple image, then maybe, just maybe, the reconstruction solver used is probably not the most appropriate one. Plainly speaking, the current implementation of the Inverse Fourier Transform with missing values, while convenient and known, may not be.enforcing the right constraint(s).
[1] Quadriwave lateral shearing interferometry for quantitative phase microscopy of living cells by Pierre Bon. Guillaume Maucort. Benoit Wattellier and Serge Monneret
[3] High resolution reflection tomographic diffractive microscopy by M. Sarmis; B. Simon; M. Debailleul; B. Colicchio; V. Georges; J. -J. Delaunay; O. Haeberlé
.JPG)


.JPG)
.JPG)
No comments:
Post a Comment