CS: Follow-up on "Compressible" Realization of Gaussian Noise

Emmanuel Candes just sent me the following:

Hi Igor,

I looked at your post today and it seems to me that you are learning about statistics of ordered independent normals :)

I suggest a simpler experiment. Take a long Gaussian vector with mean zero and variance 1 and assume that your dictionary is the identity. The best sparse approximation simply keeps the largest entries. Now in the spirit of your simulations, set a threshold at 0.25, say. That is, discard all the entries with magnitude less than 0.25. Since P(|Z| \lt 0.25) ~ 0.2, you will discard about 20% of the entries. You can also calculate the relative MSE, the average relative squared error. This will be about 4 10^-3.

Now as N increases in your experiment, it is no surprise that things ``get better''. In the limit where N is infinity, every vector will be 1-sparse in your dictionary. In fact as N gets exponentially large in the dimension, they will all be nearly 1-sparse.

Emmanuel

Thanks Emmanuel.

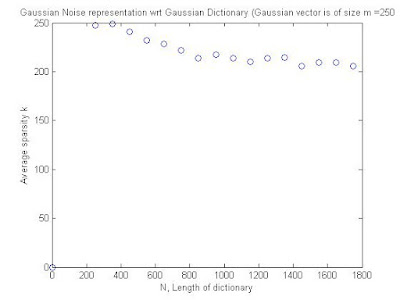
I agree with Emmanuel that asymptotically, as N grows, we have a ideal Lena problem, you know the one where one has a dictionary with an element being a full Lena. While the example of the identity dictionary is self explanatory, I am still somehow surprised at the 30 percent drop for a 1 percent accuracy shown in the previous entries. I note that this drop varies and is dependent on the solver being used. The previous entry showed the encouraging results for SL0. Here are less encouraging results for the Basis Pursuit/SPGL1.

recall that ideally, we are aiming for a figure like this one (caveat in the article, the values of N, m and k are infinite but the ratio kappa and alpha are constant).

And so the question that is interesting to consider is: given m say 250, are there solvers that can do better than SL0 for a 1 percent accuracy ? Let us recall what that figure showed for that solver: