A major challenge in ultra-wide-band (UWB) signal processing is the requirement for very high sampling rate. The recently emerging compressed sensing (CS) theory makes processing UWB signal at a low sampling rate possible if the signal has a sparse representation in a certain space. Based on the CS theory, a system for sampling UWB echo signal at a rate much lower than Nyquist rate and performing signal detection is proposed in this paper. First, an approach of constructing basis functions according to matching rules is proposed to achieve sparse signal representation because the sparse representation of signal is the most important precondition for the use of CS theory. Second, based on the matching basis functions and using analog-to-information converter, a UWB signal detection system is designed in the framework of the CS theory. With this system, a UWB signal, such as a linear frequency-modulated signal in radar system, can be sampled at about 10% of Nyquist rate, but still can be reconstructed and detected with overwhelming probability. The simulation results show that the proposed method is effective for sampling and detecting UWB signal directly even without a very high-frequency analog-to-digital converter.
As some of you may have noticed, I have an interest in using off the shelf cameras to produce a new architecture for a new kind of CS camera. While chatting, Serge Verglas, a professional photographer, mentioned to me some of the more exotic architecture he has noted with regards to cameras. Besides the lensbabies set up I refered to earlier, he told me about the hexagonal setup of pixels in Fuji cameras.

The SuperCCD honeycomb structure is featured for example in a FUJI DSLR: the Finepix S5 pro. However, as mentioned in the wikipedia entry
By contrast, Fujifilm says that 5th Generation Super CCD HR sensors are also at 45 degrees but do not interpolate. However, it omits to explain how the sensors turn the image into horizontal/vertical pixels without interpolatingSince I do not own one, I do not know if there is a RAW like format that produces values on each of the pixels as opposed to interpolated values on a regular grid. While we are on the subject of irregular sampling, I came across this picture of the organization of the three cone (color) classes in the primate retina:

I cannot help but think that the blue dots lies on some sorts of quasicrystral-like setting but hey that's just me. Irrespective, this organization is a far cry from the current Bayer pattern used in most cameras.

Let us also recall, that there is at least one model of the visual cortex where random projections are used, and while some people might object that this model is nonlinear, there are at least two examples in the CS literature where thresholding and nonlinearities are OK such as in :
- 1-bit compressed sensing and,
- the quantization as mentioned by Emmanuel Candes in one of his presentation.
Two other items attracted my attention with regards to exotic set-up and hardware:
- Some of the research at the Technion. Let us note the encryption business is earily similar to encypting with random projections.
- Axicons
An astute reader mentions the presentation of the paper referred to in yesterday's entry. I cannot state it again, this is an important paper in that it seems to be a greedy (i.e. expected to be fast) algorithm that it is a third way (besides RIP and incoherence), to find out if a measurement matrix is a good one for a certain type of CS signal. I'll add that to the big picture page. The presentation is: A New Condition for Exact ℓ1 Recovery by Charles Dossal and Gabriel Peyre

On yesterday's entry, Laurent Jacques made the following interesting statement:
Funny to see that Iterative Hard Thresholding quoted above is equivalent (but not equal) to the S-POCS algo proposed before in the Monday Morning Algos if you replace the pseudoinverse (used to project solution onto the hyperplane Phi x = y) by the transposition of the measurement matrix Phi^T
Some weeks ago, Frédéric Barbaresco, presented an unusual (at least to me) paper at ISI-GdR. He gave me the permission to post both the presentation and the preprint. The preprint is entitled: Innovative Tools for Radar Signal Processing Based on Cartan’s Geometry of SPD Matrices & Information Geometry. The abstract reads:
New operational requirements for stealth targets detection in dense & inhomogeneous clutter are emerging (littoral warfare, low altitude asymmetric threats, battlefield in urban area…). Classical Radar approaches for Doppler & Array signal processing have reached their limits. We propose new improvements based on advanced Mathematical studies on Geometry of SPD matrix (Symmetric Positive Definite matrix) and Information Geometry, using that Radar data Covariance matrices include all information of the sensor signal. First, Information Geometry allows to take into account statistics of Radar covariance matrix (by mean of Fisher information matrix used in Cramer-Rao bound) to built a robust distance, called Jensen, Siegel or Bruhat-Tits metric. Geometry on “Symmetric cones”, developed in frameworks of Lie Group and Jordan Algebra, provides new algorithms to compute Matrix Geometric Means that could be used for “matrix CFAR”. This innovative approach avoids classical drawbacks of Doppler processing by filter banks or FFT in case of bursts with very few pulses.
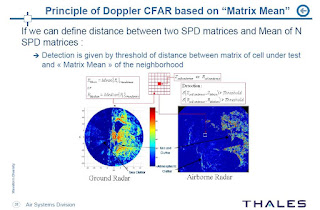
Wow. It is a manifold based signal processing that parallels similar work in Compressed Sensing with the work of (for instance) of Mike Wakin, and Richard Baraniuk (in Random Projections of Smooth Manifolds). Let us note that in image processing and by extension when used in CS (the only known example is with the Rice single pixel camera), these manifolds that embed the transformation between images are known to be discontinuous. The work around this is to use different smoothing filters at different scales in order to come back to the smooth manifold case and enable classification (Multiscale random projections for compressive classification by Marco Duarte, Mark Davenport, Michael Wakin, Jason Laska, Dharmpal Takhar, Kevin Kelly, and Richard Baraniuk).
No comments:
Post a Comment