Why You Should Care About A Compressive Sensing Approach to CT

You should care about a compressive sensing approach to CT because CT is a technology that already works and does not need the CS framework as a way to progress. Yet, there is no clear rule of thumb for doing things except in some very specific cases. I have had some on and off discussions with Emil Sidky, Dick Gordon and others about CT as of late. Clearly since there are many parameters to deal with, it is not obvious where a big improvement can come from. Emil, for instance, yesterday pointed me to his latest paper on the subject. Precisely he and his co-authors point to the fact that the number of measurements used in CT is likely to have an optimal value and therefore, there is probably no need for some new kind of Compressive Sensing CT device (Dick and I are thinking about this). I am not overly convinced by their argument ( remember the quote: The thought that disaster is impossible often leads to an unthinkable disaster) so let me expose a little bit of what I am thinking. First, let us take a look at their paper: Toward optimal X-ray flux utilization in breast CT by Jakob H. Jørgensen, Per Christian Hansen, Emil Sidky, Ingrid S. Reiser, and Xiaochuan Pan. The abstract reads:

A realistic computer-simulation of a breast computed tomography (CT) system and subject is constructed. The model is used to investigate the optimal number of views for the scan given a fixed total X-ray fluence. The reconstruction algorithm is based on accurate solution to a constrained, TV minimization problem, which has received much interest recently for sparse-view CT data.

I'll abstract the fact that they are dealing with TV reconstruction, we all know that this is not optimal, but their point is more important that there is optimal number of views. However there is no "recipe" on how to find this optimal number of views except through some computations. To put this in some compressive sensing perspective, let me recall the data used in that paper: They have a certain number of unknowns N = 1024 * 1024, their number of measurements is m = t * 1024, where t is the number of rays (or views) shot at the target et 1024 is the number of detectors (for one shot there are 1024 detectors recording one measurement each). Finally, the sparsity of the scene is k = 55000. The article  looks at several number of shots (or view) needed to get a good reconstruction. In particular, they are varying t from 128 to 512.

If this is a CS problem (at the very least it is if we focus on the sparsity of the scene) then we should put their data points on the Donoho-Tanner phase diagram to see where we are and what we should expect in terms of potential improvement. To do that, we go check to the DT website where the following figure comes from:.

In the paper set-up, we have:

• on the x-axis, the value of \delta = m/N = t * 1024/(1024*1024) = t/1024
• and on the y-axis, the value of \rho = k/m = 55000/(t*1024)

with t varying from 128 to 512.

One can notice right away that, the number of measurements (t *1024) is not important when one wants to know the intrinsic limit of a system with a grid of 1024*1024 because there is a clear relationship between \rho and \delta, namely:

\rho = 0.0524 / \delta

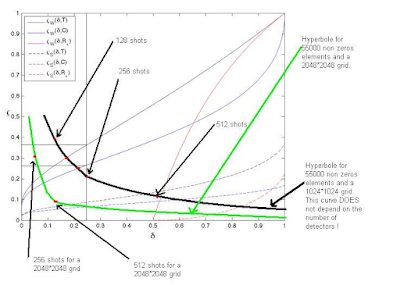
In other words, the intrinsic limit of the system is not dependent on the number of shots being fired NOR on the number of detectors. To make matters more understandable, I drew the intrinsic curve ( an hyperbole as pointed out earlier) on top of the Donoho-Tanner phase diagram in black:

The phase diagram (blue or black transition curve in the original DT phase diagram) delimits the critical number of shots needed: As one can see, this number is more than 128 but less than 256. At 256 shots (\delta =0.25), the limit of the simplex (i.e l1 regularization + additivity constraint) is (according to the form on the DT website) \rho = 0.365 when the characteristic \rho of this system is only 0.2089. So there is plenty of space.

On the graph, I also added the (green) curve where the problem is made up of a 2048 by 2048 grid. It shows that 256 shots in that configuration (with 1024 detectors) could not provide reconstruction as you'd need more measurements. In particular, you'd need either 512 shots with 1024 detectors or 256 shots with 2048 detectors.

In the CT business, you want to balance the cost associated with a large number of detectors with the  concern of reducing the radiation dose to the patient. This analysis based on the DT transition permits this trade-off study.  In short, the reason you should care about a compressive sensing approach to CT is because the DT transition can provide some direction in a way that no other rule of thumb can...Then there is the issue of noise and how the DT transition shifts as a result and how this idea of random grids can fit into this problematic but this will be for another entry.