Nuit Blanche: This Week in Compressive Sensing

Friday, September 23, 2011

This Week in Compressive Sensing

[Update: The second part of this entry led to the following entries: A stunning development in breaking the Donoho-Tanner phasetransition ? , Build it and people will come. ]

Today we have a poster : Efficient Deterministic Compressive Sensing for Images with Chirp and Reed-Muller codes.and two papers from arxiv:

One-bit compressed sensing by linear programming by Yaniv Plan, Roman Vershynin. The abstract reads:

In compressed sensing, one's goal is to recover a sparse vector from a minimal number of linear measurements. It is known that O(s log(n/s)) random measurements are sufficient to stably recover an s-sparse vector in n-dimensional space, and the solution can be obtained by convex optimization. However, in general this theory breaks down in the absence of infinite bit precision. We study maximally quantized compressed sensing in which one sees a single bit per measurement, specifically the sign of the linear measurement. We demonstrate that a simple linear program achieves accurate estimation from O(s log^2(n/s)) one-bit measurements. This result also extends to approximately sparse signals (compressible signals). Our results are universal; they imply that one measurement scheme will successfully recover all sparse vectors simultaneously. Our argument is based on solving an equivalent geometric problem on random hyperplane tessellations.

This is a new and deep geometrical insight on how to solve these problems that seems to be directly amenable to a CVX formulation. For those of you interested in this 1-bit approach with implementation that allow you to study and evaluate here is a toolbox and a demo:

The BPDQ Toolbox by David Hammond, Laurent Jacques and M. Jalal Fadili . The Basis Pursuit Dequantizers for recovery of sparse signals from quantized random measurements.
Binary Iterative Hard Thresholding (BIHT) Demo by Laurent Jacques, Jason Laska, Petros Boufounos, andRichard Baraniuk

These implementations can also be found on the big picture in compressive sensing.

Next, I am not quite sure what to think of the following result for compressive sensing reconstruction (albeit I am sure it is a new insight in statistical physics): Statistical physics-based reconstruction in compressed sensing by Florent Krzakala, Marc Mézard, François Sausset, Yifan Sun, Lenka Zdeborová. The abstract:

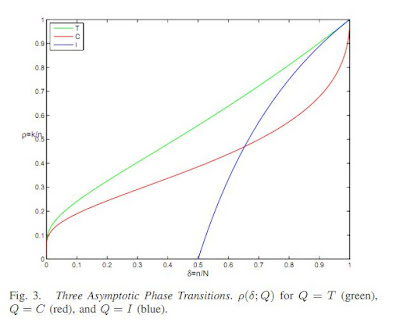
Compressed sensing is triggering a major evolution in signal acquisition. It consists in sampling a sparse signal at low rate and later using computational power for its exact reconstruction, so that only the necessary information is measured. Currently used reconstruction techniques are however limited to acquisition rates considerably higher than the true density of the signal. We design a new class of "seeded" compressed sensing measurement matrices for which a belief propagation-based algorithm achieves exact reconstruction of the signal even at measurement rates very close to the lowest possible ones. This construction is motivated by a statistical physics study of the problem and by the theory of crystal nucleation. The gain in efficiency obtained is confirmed by numerical studies of several cases.

Namely the authors show this figure with the oversampling ratio and undersampling ratio inverted:

and seem to show that their reconstruction divide the figure in two equal triangular regions where reconstruction is possible in one but not in the other and that the limiting case seems on the diagonal. I went ahead and looked up the Donoho-Tanner phase transition figure and more specifically went back to Precise Undersampling Theorems (by Donoho and Tanner) to check the phase transitions for each category of polytopes:

The green transition is for the simplex polytopes, i.e from lemma 3.1, it is for the positive solutions to underdetermined linear systems. I then put a dark line where the authors have identified a limiting case.