Convex Optimization Approaches for Blind Sensor Calibration using Sparsity /A Conjugate Gradient Algorithm for Blind Senor Calibration in Sparse Recovery

Here is a follow-up to Blind Sensor Calibration in Sparse Recovery Using Convex Optimization and Analysis Based Blind Compressive Sensing

One of the most important finding in recent years besides the idea of compressive sensing is the idea that there are sharp phase transition between parameters where a system works and doesn't work. In particular in compressive sensing, this was shown  by Jared Tanner and David Donoho in Observed universality of phase transitions in high-dimensional geometry, with implications for modern data analysis and signal processing ( see also Phase Transitions of the Regular Polytopes and Cone at University of Edinburgh) but it was really shown to be a larger property than this particular problem of sparse recovery as shown by Joel Tropp and colleagues ( .Living on the edge: A geometric theory of phase transitions in convex optimization, SAHD; Living on the edge: A geometric theory of phase transitions in convex optimization - Joel Tropp ). The importance of these results cannot be underestimated. They do two worhtwhile things in my opinion:

• they remove the asymptotic conditions that are littering the field (RIP, NSP, etc...)
• they are making it easier for hardware makers to have guidelines for actually making hardware. 

Case in point, the utilization of these phase transition curves to explore hardware calibration issues.

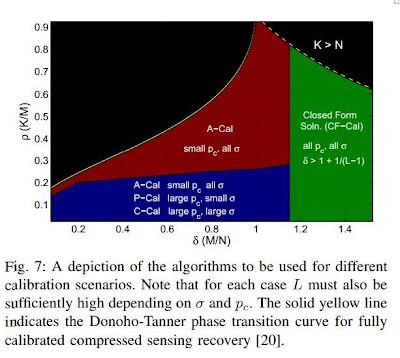
Convex Optimization Approaches for Blind Sensor Calibration using Sparsity by Cagdas Bilen, Gilles Puy, Remi Gribonval and Laurent Daudet

We investigate a compressive sensing framework in which the sensors introduce a distortion to the measurements in the form of unknown gains. We focus on blind calibration, using measurements on multiple unknown (but sparse) signals and formulate the joint recovery of the gains and the sparse signals as a convex optimization problem. The first proposed approach is an extension to the basis pursuit optimization which can estimate the unknown gains along with the unknown sparse signals. Demonstrating that this approach is successful for sufficient number of input signals except in cases where the phase shifts among the unknown gains varies significantly, a second approach is proposed that makes use of quadratic basis pursuit optimization to calibrate for constant amplitude gains with maximum variance in the phases. An alternative form of this approach is also formulated to reduce the complexity and memory requirements and provide scalability with respect to the number of input signals. Finally a third approach is formulated which combines the first two approaches for calibration of systems with any variation in the gains. The performance of the proposed algorithms are investigated extensively through numerical simulations, which demonstrate that simultaneous signal recovery and calibration is possible when sufficiently many (unknown, but sparse) calibrating signals are provided.

and A Conjugate Gradient Algorithm for Blind Senor Calibration in Sparse Recovery Hao Shen, Martin Kleinsteuber, Cagdas Bilen, Remi Gribonval

This work studies the problem of blind sensor calibration(BSC) in linear inverse problems, such as compressive sensing. It aims to estimate the unknown complex gains on eachsensor, given a set of measurements of some unknown training signals. We assume that the unknown training signalsare all sparse. Instead of solving the problem by using convex optimization, we propose a cost function on a suitablemanifold, namely, the set of complex diagonal matrices withdeterminant one. Such a construction can enhance numericalstabilities of the proposed algorithm. By exploring a globalparameterization of the manifold, we tackle the BSC problem with a conjugate gradient method. Several numericalexperiments are provided to oppose our approach to the solutions given by convex optimization and to demonstrate itsperformance.

Join the CompressiveSensing subreddit or the Google+ Community and post there !
Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.