Shedding Light on the “Grand Débat”

  

This blog post was initially featured on Medium. At LightOn, we decided to start a blog and explain what can be done with the random projections performed by our Optical Processing Unit (OPU). Since most people think an optics based system can do only images, we decided to illustrate our technology on an NLP task. Here is the article:

This article is LightOn’s AI Research (LAIR) first contribution focused on applying LightOn’s Optical Processing Unit (OPU) hardware to generic large-scale Machine Learning tasks. Today we tackle the recently released public dataset of a nation-wide public debate and our first trial in using LightOn’s OPU for a Natural Language Processing task. 

As a response to the “Gilets Jaunes” social unrest in France, President Emmanuel Macron declared the opening of a nation-wide citizen debate (“Grand Débat National”), as a way to collect the opinion of the French people on a number of subjects. Aside from public meetings taking place throughout the country, the “Grand Débat” took the form of an online platform where people could answer questions around four major themes: the environment, taxes, state organization, and democracy / citizenship. For every theme, the survey was divided in two parts: the first part featured multiple-choice surveys, while the second part included open-ended questions. A subset of the answers was made openly available by Etalab, the public organization responsible for the Open Data policy of the French government. The data can be found here.
The deadline for survey submissions to the “Grand Débat” was March 18 2019. The French government provided a first analysis on Monday, four days ago. At LightOn, we have been looking for applications of our Optical Processing Unit (OPU) to various Machine Learning problems including Natural Language Processing (NLP). We therefore took this opportunity to feature some exploratory tests on this new dataset. It should be emphasized that no one at LightOn is currently an expert in NLP: the goal of this article is only to demonstrate the kind of data processing that can be done using an OPU. We want to show how this can be done, in only a few days of work, and with no specific knowledge of NLP but a generic Machine Learning background.
The first NLP application of the OPU technology was to form sentence embeddings from word embeddings. Word embeddings are vector representation of words introduced in their modern form by Mikolov et al. (2013)¹. They have been extremely successful as a first step of virtually all NLP models: we replace vanilla one-hot-encoded vectors of dimension the size of the vocabulary with these typically 300-dimensional dense real-valued vectors. The space of word embeddings even has a sensible arithmetic, the classical example being KING — MAN + WOMAN = QUEEN. To obtain these embeddings, a linear neural network is trained to predict the surrounding words given the current word in a sliding window over a huge text corpus (this model is called skip-gram, predicting the current word from the context is also possible). At the end of the training, the projection columns of the weight matrix are the word embeddings. You can see it as a kind of shallow transfer learning, where only the first layer is pre-trained.
Sentence embeddings target similar representations, but for whole sentences. It is a much harder task than word embeddings because, while words are fixed entities and in finite and reasonable number (at least for a single language), sentences are compositional and sequential in nature. They have several degrees of freedom stemming from meaning, word choice, syntax, tone, length, etc. This diversity not only means that there is more information to encode, but also that it’s virtually impossible to save an embedding for every possible sentence. Sentence embeddings instead have to be formed on-the-fly from their constituent words.
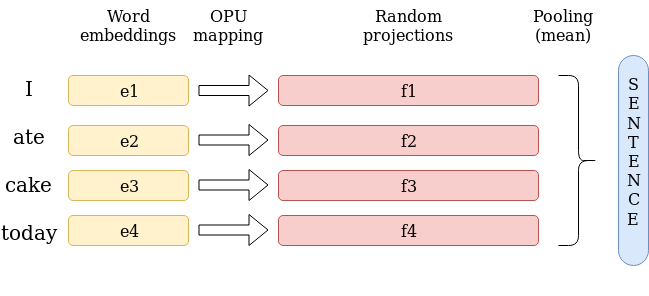
At the time of this writing, some of the leading models for sentence embeddings are SkipThought² and InferSent³. In particular, the paper that sparked our interest in sentence embeddings was the recent work of Wieting and Kiela (2019)⁴. This work shows that it is possible to obtain results on SentEval⁵ comparable to these advanced models with no training at all. One of the models used in this paper, Bag Of Random Embedding Projections(BOREP), uses random projections, which happens to be the operation an OPU excels at. As a result, we decided to give it a try. We followed BOREP but replaced the linear random projection with an OPU transform — complex-valued random projection followed by an element-wise non-linearity. The model is very simple: we get the embedding of each word in a sentence, we project it to a — much — higher dimension and then we apply a pooling function (the mean in practice) to obtain the embedding of the sentence.

The input to the current OPU prototypes -with remote access available to selected users - is a binary vector, meaning in this case that we need to use binary word embeddings. Since there is no such native embedding, we need to binarize real-valued word embeddings. For the latter, we chose fastText⁶, as it is among the best-performing word embedding method to date. To binarize the embeddings, we could use any standard binary encoding scheme. However it is hard to know a priori how destructive it would be for this kind of data. A possibly smarter thing to do is to train an autoencoder to do so. Luckily, some people did just that: binarize word embeddings using an autoencoder⁷. The associated github repo is in C, does not make use of a GPU and cannot handle large embeddings due to memory limitations, so we re-implemented it in PyTorch. It is hard to tell anything from the loss, so we evaluated our binary word embeddings directly on SentEval and obtained satisfying results for most tasks, except Semantic Textual Similarity (STS 12–16), for which there seems to be an unavoidable information loss. On a number of tasks, they performed even better than the original ones, probably because of their higher dimension. Indeed, the paper focuses on memory and computation savings, so the authors use rather low dimensional binary embeddings (up to 512 bits for an original dimension of 300 real numbers). Our goal is instead to obtain binary embeddings with the smallest possible information loss, so we went to much higher dimensions. Keep in mind that producing random projections on the OPU is essentially independent of the size — currently up to dimensions of 1 million ! In the end we used 3000 bits for each vector, so 10 bits per real number instead of 32, which seems reasonable.
Once this is done, we can actually use the OPU to form sentence embeddings using the aforementioned BOREP method. Evaluating it on SentEval gives satisfying results, in many tasks superior to that of the paper (even the Echo State Network). It should be noted that we didn’t find it useful to go above 15,000 dimensions, meaning that a high-end GPU could also have done the job in this case.
There are several reasons why increasing the dimensionality could increase performance on downstream tasks. The first is Cover’s theorem: projecting data non-linearly to a higher dimension increases the chance of them being linearly separable in the new high-dimensional space. This, of course, plays a role but the fact that a linear projection also improves performance in the Wieting and Kiela paper proves that simply adding parameters to the model already helps a lot. More interestingly, we can draw a parallel with work on hyperdimensional computing⁸. In very high-dimensional spaces (several thousand dimensions), the sheer volume available makes it possible to represent an entire dataset with no two points close to each other. The distances between two random points follow a very narrow Gaussian distribution: all points are more or less equidistant. In this setting, the mean of a few vectors is more similar to each of these vectors than any other point. The mean vector is then not merely a lossy summary of the original vectors but actually represents the set that contains them. We can thus expect the mean of the high-dimensional projections of the word embeddings to be truly more representative of the sentence than a mean computed in a lower-dimensional space, irrespective of the fact that the model used in downstream applications will have more parameters to accommodate this higher dimensionality.
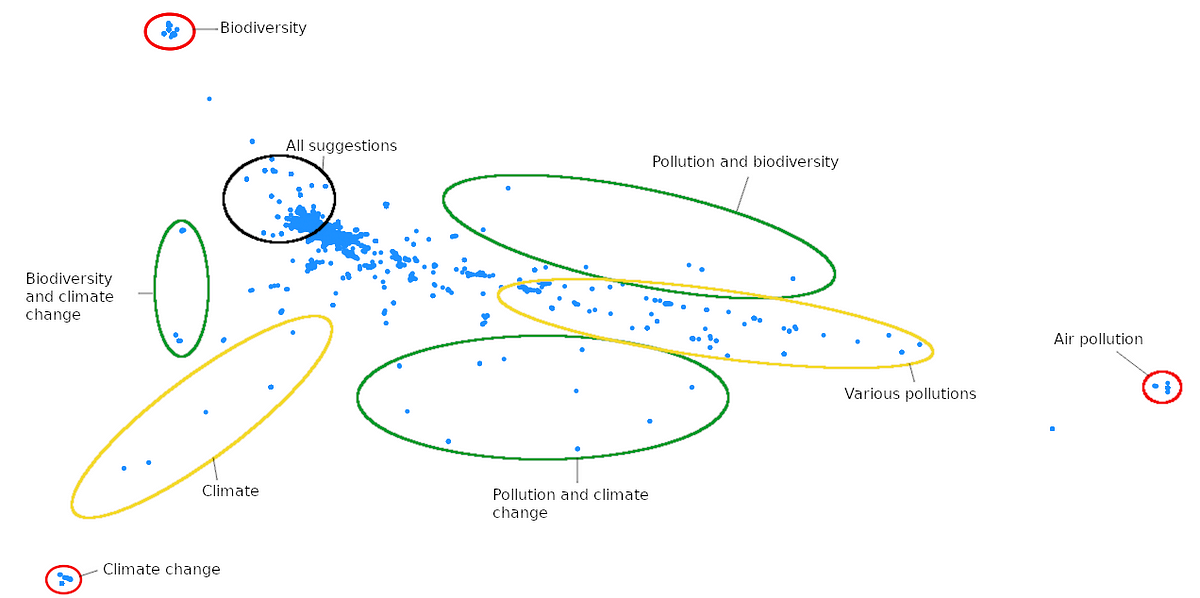
For our task of dealing with answers to open-ended questions, which is notoriously difficult, we decided that an interactive visualisation would be a nice way to explore the answers. The goal was to see clusters of similar answers as a summary of what people had to say on the matter. So we chose a specific question and formed an embedding for every answer as if it were a single sentence. From visual observations, if an answer contains several sentences, they are most of the time related, so grouping them seems a reasonable first-attempt assumption. We end up with almost a hundred thousand points in dimension 15,000 (which is also why going above 15,000 would have been problematic) and want to visualise them. A PCA to 2 or 3 dimensions doesn’t give a satisfying result, so we first keep the first 50 principal components and then use t-SNE⁹ do obtain a 2D representation of the data. The result exhibits some interesting patterns but upon inspection, we realize that the global structure doesn’t make much sense. Indeed, t-SNE only preserves local neighborhoods and loses any sense of global structure. Clusters of loosely similar answers are thus not close to each other and can even be on opposite sides of the graph. Increasing the perplexity of t-SNE is supposed to favor global structure over local one, but this had little effect, so we used another technique. t-SNE is an iterative, stochastic method requiring an initial projection. This initialization is usually random but it doesn’t have to. The first two principal components are the best 2D representation of the global structure of the data, so we use them (in practice taking the first two columns of the 50-component PCA we already computed) as the initial state of t-SNE. This allows us to preserve global structure while benefiting from the superior visualizing power of t-SNE. Follow this link to see an interactive version (in French) of this visualization. It only contains 10,000 answers, sampled uniformly without replacement, so that the interactivity remains smooth. Some annotated screenshots are shown just below. What you see are the answers to the first question of the “ecology” (environment) questionnaire. The question was:
What is to you the most important concrete problem regarding ecology ?

1. Air pollution
2. Biodiversity and species extinction
3. Climate change
4. Shore erosion
5. Other: answer in plain text

It was a semi-open question with 4 suggested answers but also the possibility to write another answer in plain text if one was not satisfied with the suggestions. Very few people answered 4, so it does not stand out on the graph, but you can clearly see answers 1, 2 and 3 circled in red on the first graph. In green are answers that mentioned two of the suggested answers and in yellow answers that gave variations of one of the suggested answers, e.g. global warming instead of climate change or water pollution instead of air pollution. A significant portion of people refused to choose and said that all suggestions were equally important.



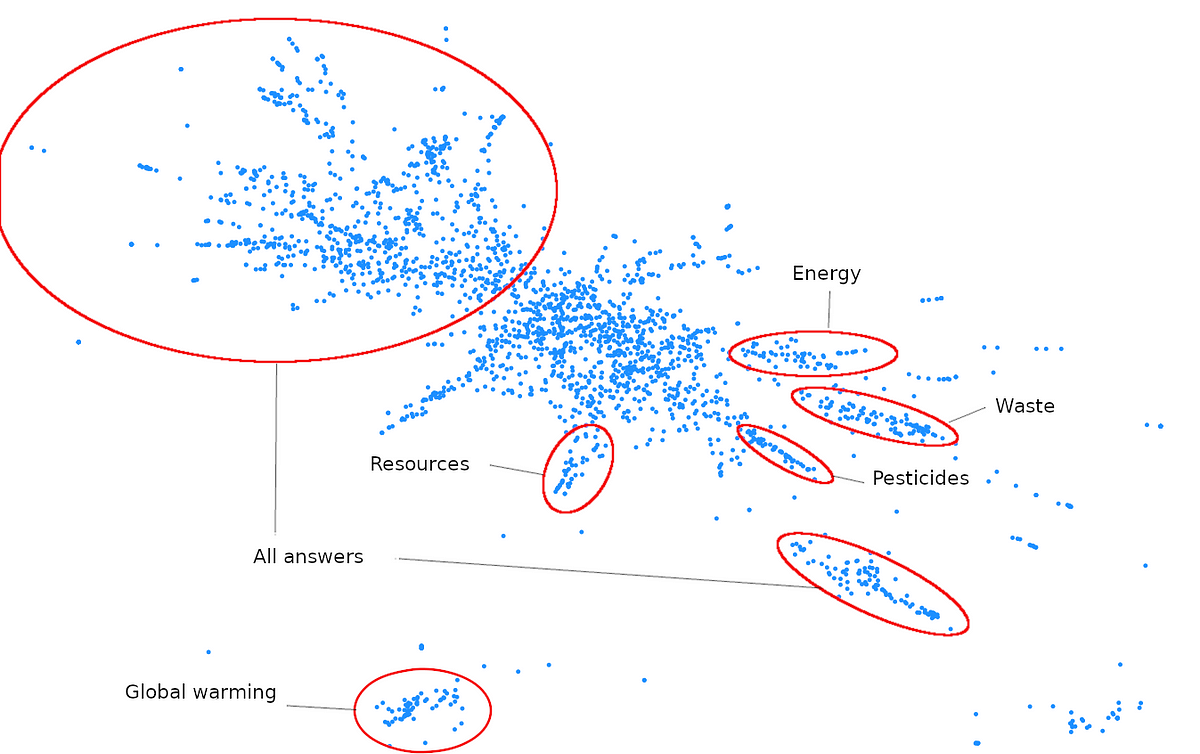
Our visualization technique mostly works with respect to our objective for short sentences, less for longer ones. These are instead gathered in the middle, where more groups can be found as you can see here:




Long answers are hard to classify as belonging to one group or another, and are likely to be far from any other answer, as mentioned before. We believe the big cloud in the middle to be an artifact of the projection, that gathers such isolated answers, more than of the embeddings.
Overall, the result is rather satisfying, given the time spent. There is, of course, much room for improvement, though, with at least three directions to explore:

• text preprocessing: we did tokenization, stop words removal and lemmatization, which are standard practices, but more thought could be put into it. For instance, a spelling corrector should help;

• multi-sentence answers: can we separate semantically independent parts of long answers to give them tags ? can we better combine the sentence embeddings of a multi-sentence answer than a simple average ?

• better sentence embeddings.

On the last point, one could, of course, use a more complex model than ours, e.g. SkipThought and InferSent. More recent models such as QuickThought¹⁰ or multi-task learning approaches have also been proposed¹¹ ¹². However, all these models are much harder to use than ours. Trained encoders are available in English but not in French, so one would have to retrain them. For supervised approaches, the data doesn’t even exist in French. SkipThought is unsupervised but takes several weeks to train. The best chance would be QuickThought but still it requires a book corpus in French and a day of training on a powerful GPU (a Titan X in the paper).
It is instead very easy to obtain satisfying results quickly with our model and OPU hardware. No training, any language works as long as word embeddings are available (fastText supports 157 languages), only the projection time (less than a minute in our case) and enough RAM to store the results are needed. The disadvantage is that the pooling function in our model loses word ordering information. The next step for us is therefore to try a time-aware model such as an Echo State Network, which was used with success in Wieting and Kiela (2019) and which can also be implemented very efficiently at large scale on an OPU¹³.
More info on LightOn’s OPU technology can be found at www.lighton.io. A remote access to an OPU through the LightOn Cloud can be granted, by invitation.


References

[1] Tomas Mikolov et al. “Efficient estimation of word representations in vector space.” arXiv preprint arXiv:1301.3781 (2013).
[2] Ryan Kiros et al. “Skip-thought vectors.” Advances in Neural Information Processing Systems. 2015.
[3] Alexis Conneau et al. “Supervised learning of universal sentence representations from natural language inference data.” arXiv preprint arXiv:1705.02364 (2017).
[4] John Wieting and Douwe Kiela. “No training required: Exploring random encoders for sentence classification.” arXiv preprint arXiv:1901.10444 (2019).
[5] Alexis Conneau and Douwe Kiela. “Senteval: An evaluation toolkit for universal sentence representations.” arXiv preprint arXiv:1803.05449 (2018).
[6] Piotr Bojanowski et al. “Enriching word vectors with subword information. CoRR abs/1607.04606.” (2016).
[7] Julien Tissier, Guillaume Gravier and Amaury Habrard. “Near-lossless Binarization of Word Embeddings.” arXiv preprint arXiv:1803.09065 (2018).
[8] Pentti Kanerva “Hyperdimensional computing: An introduction to computing in distributed representation with high-dimensional random vectors.” Cognitive computation 1.2 (2009): 139–159.
[9] Laurens van der Maaten and Geoffrey Hinton. “Visualizing data using t-SNE.” Journal of Machine Learning Research 9.Nov (2008): 2579–2605.
[10] Lajanugen Logeswaran and Honglak Lee. “An efficient framework for learning sentence representations.” arXiv preprint arXiv:1803.02893 (2018).
[11] Sandeep Subramanian et al. “Learning General Purpose Distributed Sentence Representations via Large Scale Multi-task Learning.” CoRRabs/1804.00079 (2018): n. pag.
[12] Daniel Cer et al. “Universal sentence encoder.” arXiv preprint arXiv:1803.11175 (2018).
[13] Jonathan Dong et al. “Scaling up Echo-State Networks with multiple light scattering.” 2018 IEEE Statistical Signal Processing Workshop (2018), arXiv:1609.05204

The author François Boniface, Machine Learning R&D engineer at LightOn AI Research

Join the CompressiveSensing subreddit or the Facebook page and post there !

Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.

Video: Robust and High-Dimensional Statistics workshop - Oct. 29 – Nov. 2, 2018, (Simon Institute and Kavli Foundation)

The Robust and High-Dimensional Statistics workshop is part of the Program on Foundations of Data Science sponsored by the Simons Institute for the Theory of Computing at Berkeley and the Kavli Foundation. It took place Oct. 29 – Nov. 2, 2018 in Berkeley. Thank you to the organizer to make this workshop a reality: Andrea Montanari, Emmanuel Candès, Ilias Diakonikolas, Santosh Vempala. Here are the videos:

This workshop will focus on recent developments in high-dimensional statistics, with an emphasis on different notions of robustness, the extent to which recent developments in theoretical computer science can lead to improvements with respect to traditional statistical metrics, challenges arising when the number of data points and the number of features diverge at similar rates, etc. Other potential topics are inference and causality, as well as inference after selection, i.e., data snooping and problems of multiple inference.

Robust List Decoding of Spherical Gaussians, Daniel Kane (UC San Diego)

We discuss new techniques for approximating the mean of a Gaussian in the presence of a large fraction of adversarial errors. We show that by taking advantage of higher moments of these distributions, we can obtain errors close to the information-theoretic optimum, and present an application of this to learning mixtures of spherical Gaussians.

Mixture Models, Robustness, and Sum of Squares Proofs, Jerry Li (Massachusetts Institute of Technology)

We use the Sum of Squares (SoS) method to develop a new efficient algorithm for clustering and mean estimation in well-separated high-dimensional mixture models, substantially improving upon the statistical guarantees achieved by previous efficient algorithms. In particular, we study mixtures of k distributions, where every pair of distributions has means separated by separated by at least k^epsilon for any epsilon > 0. In the special case of spherical Gaussian mixtures, we give a k^O(1/epsilon^2)-time algorithm that learns the means of the components in the mixture and accurately clusters samples from the mixture. This is the first algorithm to improve on greedy (?single-linkage?) and spectral clustering, breaking a long-standing barrier for efficient algorithms at separation k^1/4. Our techniques are based on adapting algorithmic ideas from robust statistics, and are potentially of independent interest. Our main algorithm for learning mixture models provides an entirely SoS interpretation of the convex programming framework of [Diakonikolas et al, FOCS 16]. We show that many of the proofs from that paper can be replaced with much simpler proofs using only basic concentration and Holder's inequality, which allows us to approach this problem via SoS. As a corollary of this, we also obtain improved rates for robust mean estimation in certain regimes. Joint work with Sam Hopkins (Berkeley).

Computational-Statistical Tradeoffs in Robust High-Dimensional Estimation, Ilias Diakonikolas (University of Southern California)

What is the effect of robustness on the computational complexity of high-dimensional estimation? In this talk, I will describe a technique that establishes computational-statistical tradeoffs for a range of robust estimation problems using the lens of the Statistical Query (SQ) complexity. The prototypical applications of our technique will be for the problems of robust mean and covariance estimation. The talk will be based on joint works with Daniel Kane (UCSD) and Alistair Stewart (USC).

Efficient Algorithms for Outlier-Robust Regression, Adam Klivans (University of Texas, Austin)

We give the first polynomial-time algorithm for performing linear or polynomial regression resilient to adversarial corruptions in both examples and labels. Given a sufficiently large (polynomial-size) training set drawn i.i.d. from distribution D and subsequently corrupted on some fraction of points, our algorithm outputs a linear function whose squared error is close to the squared error of the best-fitting linear function with respect to D, assuming that the marginal distribution of D over the input space is certifiably hypercontractive. This natural property is satisfied by many well-studied distributions such as Gaussian, strongly log-concave distributions and, uniform distribution on the hypercube among others. We also give a simple statistical lower bound showing that some distributional assumption is necessary to succeed in this setting. These results are the first of their kind and were not known to be even information-theoretically possible prior to our work.

Detecting Weak Signals via Hypothesis Testing, Ravi Kannan (Microsoft Research India)

Classical hypothesis testing seeks to decide whether given data is signal or noise. Likelihood ratio (LR) tests are known to minimize the probability of false positive (FP) for any given probability of false negative (FN).

We consider data which is either all noise - Eg. drawn from a standard Gaussian N(0,1) - or mostly noise with a weak signal - Eg. drawn from a Gaussian mixture: (epsilon) N(\mu,1) + (1-epsilon)N(0,1). We seek tests for which both FP and FN go to zero as the number of iid samples goes to infinity. We show essentially that ideal tests exist if the chi-squared distance between signal and noise is higher than a certain threshold.

Interestingly, it turns out that the best tests do not use LR, but a related, yet different quantity.

The proofs are simple and the result is work in progress. The talk will describe things from first principles.

Joint Work with Richard Karp.

On Using Graph Distances to Estimate Euclidean and Related Distances,  Ery Arias-Castro (UC San Diego)

Graph distances have proven quite useful in machine learning/statistics, particularly in the estimation of Euclidean or geodesic distances. The talk will include a partial review of the literature, and then present more recent developments on the estimation of curvature-constrained distances on a surface, as well as on the estimation of Euclidean distances based on an unweighted and noisy neighborhood graph.

The Importance of Better Models in Stochastic Optimization - Robustness, Fast Convergence, and Optimality, John Duchi (Stanford University)

We develop model-based methods for solving stochastic convex optimization problems, introducing the approximate-proximal point, or aProx, family, which includes stochastic subgradient, proximal point, and bundle methods. When the modeling approaches we propose are appropriately accurate, the methods enjoy stronger convergence and robustness guarantees than classical approaches, even though the model-based methods typically add little to no computational overhead over stochastic subgradient methods. For example, we show that improved models converge with probability 1 and enjoy optimal asymptotic normality results under weak assumptions; these methods are also adaptive to a natural class of what we term easy optimization problems, achieving linear convergence under appropriate strong growth conditions on the objective. Our substantial experimental investigation shows the advantages of more accurate modeling over standard subgradient methods across many smooth and non-smooth optimization problems.

Invariance, Causality and Novel Robustness, Peter Bühlmann (ETH Zürich)

Heterogeneity across different sub-populations or "homogeneous blocks" can be beneficially exploited for causal inference and novel robustness, with wide-ranging prospects for various applications. The key idea relies on a notion of probabilistic invariance or stability: it opens up new insights for formulating causality as a certain risk minimization problem with a corresponding notion of robustness. The novel methodology has connections to instrumental variable regression and robust optimization.

Generalization Bounds for Uniformly Stable Algorithms, Vitaly Feldman (Google)

Uniform stability of a learning algorithm is a classical notion of algorithmic stability introduced to derive high-probability bounds on the generalization error (Bousquet and Elisseeff, 2002). Specifically, for a loss function with range bounded in $[0,1]$, the generalization error of $\gamma$-uniformly stable learning algorithm on $n$ samples is known to be at most $O((\gamma +1/n) \sqrt{n \log(1/\delta)})$ with probability at least $1-\delta$. Unfortunately, this bound does not lead to meaningful generalization bounds in many common settings where $\gamma \geq 1/\sqrt{n}$. Here we prove substantially stronger generalization bounds for uniformly stable algorithms without any additional assumptions. First, we show that the generalization error in this setting is at most $O(\sqrt{(\gamma + 1/n) \log(1/\delta)})$ with probability at least $1-\delta$. In addition, we prove a tight bound of $O(\gamma^2 + 1/n)$ on the second moment of the generalization error. The best previous bound on the second moment of the generalization error is $O(\gamma + 1/n)$. Our proofs are based on new analysis techniques and results imply substantially stronger generalization guarantees for several well-studied algorithms. Joint work with Jan Vondrak (Stanford).

Orthogonal Machine Learning: Power and Limitations, Lester Mackey (Microsoft Research)

Double machine learning provides $\sqrt{n}$-consistent estimates of parameters of interest even when high-dimensional or nonparametric nuisance parameters are estimated at an $n^{-1/4}$ rate. The key is to employ Neyman-orthogonal moment equations which are first-order insensitive to perturbations in the nuisance parameters. We show that the $n^{-1/4}$ requirement can be improved to $n^{-1/(2k+2)}$ by employing a k-th order notion of orthogonality that grants robustness to more complex or higher-dimensional nuisance parameters. In the partially linear regression setting popular in causal inference, we show that we can construct second-order orthogonal moments if and only if the treatment residual is not normally distributed. Our proof relies on Stein's lemma and may be of independent interest. We conclude by demonstrating the robustness benefits of an explicit doubly-orthogonal estimation procedure for treatment effect.

Some Problems of Robust High-dimensional Statistics, Gilad Lerman (University of Minnesota)

The talk will first review the problem of robust subspace recovery, which seeks an underlying low-dimensional subspace in a data set that is possibly corrupted with outliers. The emphasis will be on surveying existing theoretical guarantees and tradeoffs. New results for adversarial outliers will also be mentioned. Following this, other related problems will be discussed, along with new results for one of these problems.

TAP Free Energy, Spin Glasses, and Variational Inference, Zhou Fan (Yale University)

We consider the Sherrington-Kirkpatrick model of spin glasses with ferromagnetically biased couplings. For a specific choice of the couplings mean, the resulting Gibbs measure is equivalent to the Bayesian posterior for a high-dimensional estimation problem known as "Z2 synchronization". Statistical physics suggests to compute the expectation with respect to this Gibbs measure (the posterior mean in the synchronization problem), by minimizing the so-called Thouless-Anderson-Palmer (TAP) free energy, instead of the mean field (MF) free energy. We prove that this identification is correct, provided the ferromagnetic bias is larger than a constant (i.e. the noise level is small enough in synchronization). Namely, we prove that the scaled l_2 distance between any low energy local minimizers of the TAP free energy and the mean of the Gibbs measure vanishes in the large size limit. Our proof technique is based on upper bounding the expected number of critical points of the TAP free energy using the Kac-Rice formula.

A Modern Maximum-Likelihood Theory for High-Dimensional Logistic Regression, Pragya Sur (Stanford University)

Logistic regression is arguably the most widely used and studied non-linear model in statistics. Classical maximum likelihood theory provides asymptotic distributions for the maximum likelihood estimate (MLE) and the likelihood ratio test (LRT), which are universally used for inference. Our findings reveal, however, when the number of features p and the sample size n both diverge, with the ratio p/n converging to a positive constant, classical results are far from accurate. For a certain class of logistic models, we observe, (1) the MLE is biased, (2) variability of the MLE is much higher than classical results and (3) the LRT is not distributed as a Chi-Squared. We develop a new theory that quantifies the asymptotic bias and variance of the MLE, and characterizes asymptotic distribution of the LRT under certain assumptions on the distribution of the covariates. Empirical results demonstrate that our asymptotic theory provides extremely accurate inference in finite samples. These novel results depend on the underlying regression coefficients through a single scalar, the overall signal strength, which can be estimated efficiently. This is based on joint work with Emmanuel Candes and Yuxin Chen.

Robustness in High-Dimensional Inference Tasks, Jelena Bradic (UC San Diego)

This talk studies hypothesis testing and confidence interval construction in high-dimensional linear models where robustness is view in the context of whether the data is truly sparse. We will show new concepts of uniform and essentially uniform non-testability that allow the study of the limitations of tests across a broad set of alternatives. Uniform non-testability identifies an extensive collection of alternatives such that the power of any test, against any alternative in this group, is asymptotically at most equal to the nominal size, whereas minimaxity shows the existence of one, particularly "bad" alternative. Implications of the new constructions include new minimax testability results that in sharp contrast to existing results do not depend on the sparsity of the model parameters and are therefore robust. We identify new tradeoffs between testability and feature correlation. In particular, we show that in models with weak feature correlations minimax lower bound can be attained by a confidence interval whose width has the parametric rate regardless of the size of the model sparsity.

Controlling FDR While Highlighting Selected Discoveries, Chiara Sabatti (Stanford University)

In modern science, often data collection precedes the careful specification of hypotheses. Large datasets are mined, testing a large number of possible hypotheses, with the goal of identifying those that hold promise for follow-up. In this framework, controlling the False Discovery Rate is an appropriate criterion to avoid investing time and resources into non viable leads. In many contexts, the initial large collection of explored hypotheses is somewhat redundant: in an effort to maximize power, the same scientific statement can be probed with a number of related hypotheses. For example, the association between a phenotype and one genetic locus can be investigated by exploring the association between the phenotype and many genetic variants in the locus. After the first pass through the data is completed, however, and it is time to take stock of the identified scientific leads, this redundancy is corrected: in the example above, rather than reporting all variants associated with a phenotype, scientists routinely report only a ?lead? variant, selected to represent the entire locus. Because the false discovery proportion is crucially defined with reference to the total set of discoveries, however, these subsets of discoveries identified post-hoc are not equipped with guarantees of FDR control. To overcome this problem, we note that if the criterion with which discoveries will be filtered can be specified in advance, it is possible to modify the Benjamini Hochberg procedure to result in a focused set of discoveries with FDR guarantees. Our framework allows not only subsetting of discoveries, but also their prioritization with weights reflecting the extent to which they provide insight into distinct scientific questions. We illustrate our methodology with examples from gene set enrichment on the Gene Ontology, a collection of hypotheses organized in a directed acyclic graph.

The talk will be based on joint work with Eugene Katsevich (Stanford) and Marina Bogomolov (Technion).

The Robustness of Controlling the False Discovery Rate, Weijie Su (University of Pennsylvania)

The Benjamin--Hochberg (BH) procedure and many of its generalizations are empirically observed to control the false discovery rate (FDR) much beyond the regimes that are known to enjoy provable FDR control. To address this gap, this talk introduces some new results that imply the robustness of the BH procedure and certain related procedures for FDR control. First, we show that FDR control is maintained up to a small multiplicative factor under arbitrary dependence between false null test statistics and independent true null test statistics. The proof technique is based on a new backward submartingale argument. Next, we further extend the FDR control to the case where the null test statistics exhibit certain positive dependence, implying that the null distribution plays an essential role in FDR control. We conclude the talk by introducing a weak version of FDR control for which the BH procedure is robust against any adversarial false null test statistics. Part of this talk is based on joint work with Cynthia Dwork (Harvard) and Li Zhang (Google).

A Flexible Framework for Hypothesis Testing in High-Dimensions,  Adel Javanmard (University of Southern California)

We consider linear regression in the high-dimensional regime where the number of parameters exceeds the number of samples (p greater than n) and assume that the high-dimensional parameters vector is sparse. We develop a framework for testing general hypotheses regarding the model parameters. Our framework encompasses testing whether the parameter lies in a convex cone, testing the signal strength, and testing arbitrary functionals of the parameter. We show that the proposed procedure controls the false positive rate and also analyze the power of the procedure. Our numerical experiments confirm our theoretical findings and demonstrate that we control false positive rate near the nominal level, and have high power. By duality between hypotheses testing and confidence intervals, the proposed framework can be used to obtain valid confidence intervals for various functionals of the model parameters. For linear functionals, the length of confidence intervals is shown to be minimax rate optimal. [This talks is based on a joint work with Jason Lee.]

Lightning Talks

Robust Sparse Covariance Estimation by Thresholding Tyler's M-estimator, Boaz Nadler (Weizmann Institute of Science)

Estimating a high-dimensional sparse covariance matrix from a limited number of samples is a fundamental problem in contemporary data analysis. Most proposals to date, however, are not robust to outliers or heavy tails. Towards bridging this gap, we consider estimating a sparse shape matrix from n samples following a possibly heavy tailed elliptical distribution. We propose estimators based on thresholding either Tyler's M-estimator or its regularized variant. We prove that under suitable conditions the regularized variant can be computed efficiently in practical polynomial time. Furthermore, we prove that in the joint limit as dimension p and sample size n tend to infinity with p/n tending to a constant, our proposed estimators are minimax rate optimal. Results on simulated data support our theoretical analysis.

Sub-Gaussian Mean Estimation in Polynomial Time, Samuel Hopkins (UC Berkeley)

We study polynomial time algorithms for estimating the mean of a d-dimensional random vector X from n independent samples X1,?,Xn when X may be heavy-tailed. In particular, we assume only that X has finite mean and covariance. In this setting, the radius of confidence intervals achieved by the empirical mean are large compared to the case that X is Gaussian or sub-Gaussian. We offer the first polynomial time algorithm to estimate the mean with sub-Gaussian-style confidence intervals even when X has only finite second moments. Our algorithm is based on a new semidefinite programming relaxation of a high-dimensional median. Previous estimators which assumed only existence of O(1) moments of X either sacrifice sub-Gaussian performance or are only known to be computable via brute-force search procedures requiring exp(d) time.

Robust Estimation and Generative Adversarial Nets, Chao Gao (University of Chicago)

Robust estimation under Huber's $\epsilon$-contamination model has become an important topic in statistics and theoretical computer science. Rate-optimal procedures such as Tukey's median and other estimators based on statistical depth functions are impractical because of their computational intractability. In this talk, I will discuss an intriguing connection between f-GANs and various depth functions through the lens of f-Learning. Similar to the derivation of f-GAN, I will show that these depth functions that lead to rate-optimal robust estimators can all be viewed as variational lower bounds of the total variation distance in the framework of f-Learning. This connection opens the door of computing robust estimators using tools developed for training GANs. In particular, I will show that a JS-GAN that uses a neural network discriminator with at least one hidden layer is able to achieve the minimax rate of robust mean and covariance matrix estimation under Huber's $\epsilon$-contamination model. Interestingly, the hidden layers for the neural net structure in the discriminator class is shown to be necessary for robust estimation.

Can Non-Convex Optimization be Robust?, Rong Ge (Duke University)

Optimizing a non-convex function is hard in general. Existing analysis for non-convex optimization then relies on problem specific structures that may not be robust to adversarial perturbations. In this talk, we will see two scenarios where the standard non-convex optimization techniques are not robust, and show how to modify the algorithms to handle adversarial perturbations. The first scenario considers the matrix completion problem against a semi-random adversary that can reveal more entries of the matrix. Although this weak adversary is harmless to convex relaxations, we show that it can ruin non-convex approaches, and give a fast algorithm to fix this problem. The second scenario considers the more general setting where one does not have access to the exact function to optimize, where we show that it is still possible to find an approximate local optimal solution. Based on joint works with Yu Cheng, Chi Jin, Lydia Liu, Michael I. Jordan.

Semi-Random Models and Robustness in Unsupervised Learning, Aravindan Vijayaraghavan (Northwestern University)

Probabilistic models are widely used in statistical inference, and for understanding the computational tractability of several unsupervised learning tasks. However, a common criticism of most existing learning algorithms is that their guarantees strongly rely on the unrealistic assumption that the instance is generated exactly from the model. Semi-random models provide a framework to reason about robustness of algorithms to modeling errors by incorporating both adversarial and random choices in instance generation. In this talk, I will describe new semi-random models for two different problems in unsupervised learning: dictionary learning, and clustering mixtures of Gaussians. In dictionary learning the task is to learn a hidden incoherent basis/dictionary A given data Y=AX that represents unknown sparse linear combinations (corresponding to columns of X) of the basis elements. Existing algorithms learn A and X efficiently, assuming strong distributional assumptions about both the supports of the columns of X and the values of these non-zero entries. In the first part of the talk, I will describe a more general semi-random model for dictionary learning aimed at capturing almost arbitrary distributions for the sparse supports, and give a new polynomial time algorithm for learning incoherent over-complete dictionaries under the semi-random model. Finally (time permitting), I will describe a natural semi-random model for k-means clustering that generalizes mixtures of k Gaussians, and demonstrate how the Lloyds algorithm successfully recovers the ground-truth clustering up to near optimal accuracy. Based on joint works with Pranjal Awasthi.

Optimally Weighted PCA for High-Dimensional Heteroscedastic Data, Laura Balzano (University of Michigan)

Modern applications increasingly involve high-dimensional and heterogeneous data, e.g., datasets formed by combining numerous measurements from myriad sources. Principal Component Analysis (PCA) is a classical method for reducing dimensionality by projecting data onto a low-dimensional subspace capturing most of their variation, but it does not robustly recover underlying subspaces in the presence of heteroscedastic noise. Specifically, PCA suffers from treating all data samples as if they are equally informative. We will discuss the consequences of this on performance, which lead us naturally to consider weighting PCA in such a way that we give less influence to samples with larger noise variance. Doing so better recovers underlying principal components, but precisely how to choose the weights turns out to be an interesting problem. Surprisingly, we show that whitening the noise by using inverse noise variance is sub-optimal. Our analysis provides expressions for the asymptotic recovery of underlying low-dimensional components from samples with heteroscedastic noise in the high-dimensional regime. We derive optimal weights and characterize the performance of optimally weighted PCA. This is work in collaboration with David Hong and Jeff Fessler.

How Many Directions Determine a Shape: A VC Theory for Modulii Spaces of Shapes, Sayan Mukherjee (Duke University)

We study transformations of shapes into representations that allow for analysis using standard statistical tools. The transformations are based on Euler integration and are of interest for their mathematical properties as well as their applications to science and engineering, because they provide a way of summarizing shapes in a topological, yet quantitative, way. By using an inversion theorem, we show that both transforms are injective on the space of shapes---each shape has a unique transform. By making use of a stratified space structure on the sphere, induced by hyperplane divisions, we prove additional uniqueness results in terms of distributions on the space of Euler curves. The main theoretical result provides the first (to our knowledge) finite bound required to specify any shape in certain uncountable families of shapes, bounded below by curvature. This result is perhaps best appreciated in terms of shattering number or the perspective that any point in these particular moduli spaces of shapes is indexed using a tree of finite depth. We also show how these transformations can be used in practice for medical imaging applications as well as for evolutionary morphology questions.

Scale Calibration for High-Dimensional Robust Regression, Po-Ling Loh (University of Wisconsin, Madison)

We present a new method for high-dimensional linear regression when a scale parameter of the error is unknown. The proposed estimator is based on a penalized Huber M-estimator, for which theoretical results on estimation error have recently been proposed in high-dimensional statistics literature. However, variance of the error term in the linear model is intricately connected to the parameter governing the shape of the Huber loss. The main idea is to use an adaptive technique, based on Lepski's method, to overcome the difficulties in solving a joint nonconvex optimization problem with respect to the location and scale parameters.

k-means and k-medians under Dimension Reduction, Yury Makarychev (Toyota Technological Institute at Chicago)

Consider an instance of Euclidean k-means or k-medians clustering. We prove that a dimension reduction projection onto a space of dimension d ~ log k preserves the cost of the optimal clustering within a factor of 1 + epsilon w.h.p. Crucially, the dimension d does not depend on the total number of points n in the instance. The result also applies to other variants of the k-clustering problem. The result strengthens the result by Cohen, Elder, Musco, Musco, and Persu, who showed that the value of k-means is approximately preserved when d ~ k. No bounds on d were previously known for k-medians. Joint work with Konstantin Makarychev and Ilya Razenshteyn.

Efficient Profile Maximum Likelihood for Universal Symmetric Property Estimation, Moses Charikar (Stanford University)

Symmetric properties of distributions arise in multiple settings. For each of these, separate estimators and analysis techniques have been developed. Recently, Orlitsky et al showed that a single estimator that maximizes profile maximum likelihood (PML) is sample competitive for all symmetric properties. Further, they showed that even a 2^{n^{1-delta}}-approximate maximizer of the PML objective can serve as such a universal plug-in estimator. (Here n is the size of the sample). Unfortunately, no polynomial time computable PML estimator with such an approximation guarantee was known. We provide the first such estimator and show how to compute it in time nearly linear in n. We also present some preliminary experimental results. Joint work with Kiran Shiragur and Aaron Sidford.

Realizing Robustness, Gautam Kamath (Massachusetts Institute of Technology)

Over the last few years, there has been significant theoretical work in robust high-dimensional statistical estimation. These results seem aligned with modern goals in practical machine learning, where high-dimensional data is ubiquitous, and robustness and security are paramount. This raises the question: are these advances purely theoretical, or can we reap their benefits in the real world? In this talk, I will describe some first steps towards answering this question positively, including evidence that these theoretical advances may be realizable. I will discuss applications to exploratory data analysis and robust stochastic optimization on synthetic and real-world datasets.

Based on joint works with Ilias Diakonikolas, Daniel Kane, Jerry Li, Ankur Moitra, Jacob Steinhardt, and Alistair Stewart. Papers available at https://arxiv.org/abs/1703.00893 and https://arxiv.org/abs/1803.02815.

Join the CompressiveSensing subreddit or the Google+ Community or the Facebook page and post there !
Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.

Video: Randomized Numerical Linear Algebra and Applications Workshop - Sep. 24 – Sep. 27, 2018, (Simon Institute and Kavli Foundation)

The Randomized Numerical Linear Algebra and Applications workshop that took place Sep. 24 – Sep. 27, 2018 at the Simons Institute for the theory of Computing. Thanks to the organizers for the workshop: Petros Drineas, Ken Clarkson ,Prateek Jain, Michael Mahoney 

Here are the videos and some slides. 

Randomized Numerical Linear Algebra: Overview, Petros Drineas (Purdue University)

The introduction of randomization in the design and analysis of algorithms for matrix computations (such as matrix multiplication, least-squares regression, the Singular Value Decomposition (SVD), etc.) over the past 20 years provided a new paradigm and a complementary perspective to traditional numerical linear algebra approaches. These novel approaches were motivated by technological developments in many areas of scientific research that permit the automatic generation of large data sets, which are often modeled as matrices. In this talk, we will present a brief overview of Randomized Numerical Linear Algebra (RandNLA).

Randomized Least Squares Regression: Combining Model- and Algorithm-Induced Uncertainties, Ilse Ipsen (North Carolina State University)

We consider the solution of full-rank column regression problems, arising from Gaussian linear models, by randomized (row-wise sampling and sketching) algorithms. Motivated by the ground breaking work of Ma, Mahoney and Yu, we analyze expectation and variance of the minimum-norm solution with regard to both, model- and algorithm-induced uncertainties. Our expressions are exact, hold for general sketching matrices, and make no assumptions on the rank of the sketched matrix. We show that the relative differences between the total bias and variance, compared to the model bias and variance, respectively, are governed by two factors: (i) the expected rank deficiency of the sketched matrix, and (ii) the expected difference between projectors associated with the original and the sketched problems. The structural perturbation bounds imply that least squares problems are less sensitive to multiplicative perturbations than to additive perturbations. This is joint work with Jocelyn Chi.

Advanced Techniques for Low-Rank Matrix Approximation, Ming Gu (UC Berkeley)

Low-rank matrix approximations have become a technique of central importance in large scale data science. In this talk, we discuss a set of novel low-rank matrix approximation algorithms that are tailored for all levels of accuracy requirements for maximum computational efficiency. These algorithms include spectrum-revealing matrix factorizations that are optimal up to dimension-dependent constants, and an efficient truncated SVD (singular value decomposition) that is accurate up to a given tolerance. We provide theoretical error bounds and numerical evidence that demonstrate the superiority of our algorithms over existing ones, and show their usefulness in a number of data science applications.

Recent Advances in Positive Semidefinite Matrix Approximation, Cameron Musco (Microsoft Research New England)

In this talk, I will discuss recent advances in sampling methods for positive semidefinite (PSD) matrix approximation. I will start by discussing how fast leverage score approximation schemes can be combined with the popular Nystrom method for PSD kernel matrix approximation. These techniques yield the first provably accurate, linear time approximation algorithms for fundamental kernel methods like kernel ridge regression and kernel PCA, avoiding a traditional quadratic time bottleneck. I will then discuss how the same sampling techniques can be leveraged to give a surprising result: a relative error low-rank approximation to any positive semidefinite matrix can be computed in sublinear time, without any assumptions on incoherence or condition number. This result demonstrates the ability of randomized methods to exploit the structure of PSD matrices and go well beyond what is possible with traditional algorithmic techniques. I will conclude with a discussion of open questions, especially focused on oblivious sketching methods for kernel matrices.

Reconstructing Continuous Signals via Leverage Score Sampling, Chris Musco (Princeton University)

Reconstructing signals based on a small number of potentially noisy samples is a fundamental problem in signal processing. In practice, we are often interested in signals with ``simple'' Fourier transforms -- e.g. those involving frequencies within a bounded range, a small number of frequencies, or a few blocks of frequencies (bandlimited, sparse, and multiband signals, respectively). We generally find that "simpler" signals require fewer samples to learn. In this talk, I will introduce a general framework for learning continuous signals that formalizes this tradeoff between sample complexity and simplicity. Our framework is based on a connection between the signal reconstruction problem, low-rank matrix approximation, and randomized numerical linear algebra. In particular, we use tools based on leverage score sampling, and show that the number of samples required for learning a signal depends on a natural statistical dimension parameter related to these scores. Using this framework, I will also present a simple and efficient algorithm for signal reconstruction. For well-studied classes of signals (bandlimited, sparse, and multiband) our algorithm essentially matches the runtime and sample complexity of state-of-the-art methods. At the same time, it extends to a much broader class of ``simple'' signals. The main computation cost of our method is a black-box call to any existing algorithm for kernel ridge regression.

Asympirical Analysis: Theory Informs Practice, Ping Ma (University of Georgia)

Large samples have been generated routinely from various sources. Classic statistical and analytical methods are not well equipped to analyze such large samples due to expensive computational costs. In this talk, I will present an asympirical (asymptotic + empirical) analysis in large samples. The proposed method can significantly reduce computational costs in high-dimensional and large-scale data. We show the estimator based on the proposed methods achieves the optimal convergence rate. Extensive simulation studies will be presented to demonstrate numerical advantages of our method over competing methods. I will further illustrate the empirical performance of the proposed approach using two real data examples.

How Randomized Analysis Can Help Us Do “Data Science:” Examples in Deep Learning and Graph Analysis, Fred Roosta (University of Queensland)

Randomized algorithms have shown great success in many large-scale applications. However, beyond algorithmic advantages, randomization can offer insight in understanding many data scientific models. In this talk, we discuss two such examples.
In the context of analyzing neural networks, we show how randomized analysis can be used to answer questions such as “why training neural networks gets harder as the depth of the network increases?” and “what could potentially be appropriate strategies for initialization of weights in the training process?”
We then discuss an example where such style of analysis can help study graph spectral clustering algorithms. In particular, we show that, under certain assumptions, given an existing clustering, with high probability, one can efficiently and yet accurately, perform an out-of-sample extension to observations not seen in the initial clustering procedure.

Why Deep Learning Works: Implicit Self-Regularization in Deep Neural Networks, Michael Mahoney (International Computer Science Institute and UC Berkeley)

Random Matrix Theory (RMT) and Randomized Numerical Linear Algebra (RandNLA) are applied to analyze the weight matrices of Deep Neural Networks (DNNs), including both production quality, pre-trained models and smaller models trained from scratch. Empirical and theoretical results clearly indicate that the DNN training process itself implicitly implements a form of self-regularization, implicitly sculpting a more regularized energy or penalty landscape. In particular, the empirical spectral density (ESD) of DNN layer matrices displays signatures of traditionally-regularized statistical models, even in the absence of exogenously specifying traditional forms of explicit regularization. Building on relatively recent results in RMT, most notably its extension to Universality classes of Heavy-Tailed matrices, and applying them to these empirical results, we develop a theory to identify 5+1 Phases of Training, corresponding to increasing amounts of implicit self-regularization. For smaller and/or older DNNs, this implicit self-regularization is like traditional Tikhonov regularization, in that there appears to be a ``size scale'' separating signal from noise. For state-of-the-art DNNs, however, we identify a novel form of heavy-tailed self-regularization, similar to the self-organization seen in the statistical physics of disordered systems. This implicit self-regularization can depend strongly on the many knobs of the training process. In particular, by exploiting the generalization gap phenomena, we demonstrate that we can cause a small model to exhibit all 5+1 phases of training simply by changing the batch size. This demonstrates that---all else being equal---DNN optimization with larger batch sizes leads to less-well implicitly-regularized models, and it provides an explanation for the generalization gap phenomena.

Stochastic Quasi-Gradient Methods: Variance Reduction via Jacobian Sketching, Peter Richtarik (University of Edinburgh)

We develop a new family of variance reduced stochastic gradient descent methods for minimizing the average of a very large number of smooth functions. Our method---JacSketch---is motivated by novel developments in randomized numerical linear algebra, and operates by maintaining a stochastic estimate of a Jacobian matrix composed of the gradients of individual functions. In each iteration, JacSketch efficiently updates the Jacobian matrix by first obtaining a random linear measurement of the true Jacobian through (cheap) sketching, and then projecting the previous estimate onto the solution space of a linear matrix equation whose solutions are consistent with the measurement. The Jacobian estimate is then used to compute a variance-reduced unbiased estimator of the gradient, followed by a stochastic gradient descent step. Our strategy is analogous to the way quasi-Newton methods maintain an estimate of the Hessian, and hence our method can be seen as a {\em stochastic quasi-gradient method}. Indeed, quasi-Newton methods project the current Hessian estimate onto a solution space of a linear equation consistent with a certain linear (but non-random) measurement of the true Hessian. Our method can also be seen as stochastic gradient descent applied to a {\em controlled stochastic optimization reformulation} of the original problem, where the control comes from the Jacobian estimates. We prove that for smooth and strongly convex functions, JacSketch converges linearly with a meaningful rate dictated by a single convergence theorem which applies to general sketches. We also provide a refined convergence theorem which applies to a smaller class of sketches, featuring a novel proof technique based on a {\em stochastic Lyapunov function}. This enables us to obtain sharper complexity results for variants of JacSketch with importance sampling. By specializing our general approach to specific sketching strategies, JacSketch reduces to the celebrated stochastic average gradient (SAGA) method, and its several existing and many new minibatch, reduced memory, and importance sampling variants. Our rate for SAGA with importance sampling is the current best-known rate for this method, resolving a conjecture by Schmidt et al (2015). The rates we obtain for minibatch SAGA are also superior to existing rates. Moreover, we obtain the first minibatch SAGA method with importance sampling. This is joint work with Robert M. Gower (Telecom ParisTech) and Francis Bach (INRIA). https://arxiv.org/abs/1805.02632

Randomized Riemannian Preconditioning for Quadratically Constrained Problems, Haim Avron (Tel Aviv University)

We consider optimization problems of the form max f(x) s.t. x^T B x=1 where B is a symmetric positive definite matrix which is the Gram matrix of some input n-by-d data matrix X. This problem naturally occurs in quite a few application, such as finding the largest or smallest singular value, linear discriminant analysis and canonical correlation analysis. Since the constraint set is a manifold, Riemannian optimization is natural tool for tackling such problems. However, the prevalent method in which this method is materilized leads to an O(nd^2) cost, which is not attractive if n is large and/or X is sparse. The underlying reason is that these methods are based on a Riemannian metric that require the factorization of the Gram matrix B. We propose to use an alternative metric which is based on randomized precoditioning of X (e.g. the construction used in Blendenpik). Theoretical and empirical aspects will be discussed.

Convergence Theory for Iterative Eigensolvers, Mark Embree (Virginia Tech University)

Randomized methods for computing eigenvalues of large matrices are influenced by a number of fundamental spectral properties that affect algorithm performance and the quality of the resulting answers. Should one gauge convergence by eigenvalue errors, residual norms, or subspace angles? What matrix properties dictate the convergence rate? How does performance depend on the location of the sought-after eigenvalues, relative to the rest of the spectrum? How sensitive are eigenvalues and eigenvectors to changes in the matrix? How does such sensitivity influence convergence? We shall address these questions in the context of traditional (deterministic) eigensolvers, in the hope that such an overview will provide a helpful framework for designers of randomized algorithms.

Randomized Algorithms for Computing Full Matrix Factorizations, Gunnar Martinsson (University of Texas at Austin)

At this point in time, we understand fairly well how randomized projections can be used to very efficiently compute a low rank approximation to a given matrix. We have seen that randomized methods are often substantially faster than traditional deterministic methods, and that they enable the processing of matrices that are simply too large to be handled using traditional deterministic methods. In this talk, we will describe how randomization can also be used to accelerate the computation of a *full* factorization (e.g. a column pivoted QR decomposition) of a matrix. These methods achieve high speed primarily by reducing the amount of communication that is required, as compared to existing methods. This makes them particularly competitive in communication constrained environments such as data stored out-of-core, GPU computing, distributed memory machines, etc. While the methods presented were developed primarily for the purpose of computing a full factorization, they are also very convenient to use for computing partial factorizations in situations where we have no prior information about the numerical rank of the input matrix.

Applying Randomized Methods for Zonotope Enumeration and Monte Carlo Methods for Solving Linear Systems, David Gleich (Purdue University)

I'll discuss our experience in using randomized methods to sample the vertices of a zonotope, which arose when we were studying fast algorithm to solve low-rank correlation clustering problems. I'll also discuss some experience with a new type of Monte Carlo algorithms that appears to have better empirical convergence properties and better parallalization potential when solving linear systems of equations. This work is based on the following papers: https://arxiv.org/abs/1611.07305 and https://arxiv.org/abs/1608.04361

Error Estimation for Randomized Numerical Linear Algebra: Bootstrap Methods, Miles Lopes (UC Davis)

In recent years, many randomized algorithms have been proposed for computing approximate solutions to large-scale problems in numerical linear algebra. However, the user rarely knows the actual error of a randomized solution. For this reason, it is common to rely on theoretical worst-case error bounds as a source of guidance. As a more practical alternative, we propose bootstrap methods to obtain direct error estimates for randomized solutions. Specifically, in the contexts of matrix multiplication and least-squares, we show that bootstrap error estimates are theoretically justified, and incur modest computational cost.

Scalable Algorithmic Primitives for Data Science, Richard Peng (Georgia Institute of Technology)

The study of large scale matrices and networks often utilize high-level algorithmic primitives for them: tools such as solving linear systems and computing eigenvectors are now taught in courses on machine learning and statistics. On the other hand, the rapid growth in data sizes exposed significant shortcomings in the scalability of such primitives, and accentuated the need for provably efficient algorithms. Here the Laplacian paradigm for graph algorithms has led to improvements on many fundamental problems in scientific computing and combinatorial optimization, as well as highly efficient code packages that have been applied to image processing and data mining. These works started from the rich mathematical connections between graphs and matrices provided by spectral graph theory, but increasingly rely on fine-grained coupling between combinatorial and numerical components. This talk will discuss some of the key ideas in these algorithms, with focus on the uses of efficient structure-preserving sampling and high dimensional concentration.

Hessian Matrix Inversion in 10^10 Dimensions with Parametric Bootstraps, Uros Seljak (UC Berkeley)

A common statistical analysis problem is to determine the mean and the variance of a (few) parameter(s), marginalizing over a large number of latent variables, which are all correlated, so that the Hessian is a full rank matrix. This requires inverting the Hessian, which becomes impossible using linear algebra in a very high number of dimensions. I will present a method to obtain the Hessian inverse matrix elements using parametric bootstrap samples (simulations), where only a few samples already give a reliable estimate. I will present an application of this method to the cosmological data analysis problem, where we operate with up to 1010 fully correlated observations of galaxy positions, and we wish to determine a handful of cosmological parameters.

Ridge Regression and Deterministic Ridge Leverage Score Sampling, Shannon McCurdy (UC Berkeley)

Ridge leverage scores provide a balance between low-rank approximation and regularization, and are ubiquitous in randomized linear algebra and machine learning. Deterministic algorithms are also of interest in the moderately big data regime, because deterministic algorithms provide interpretability to the practitioner by having no failure probability and always returning the same results. We provide provable guarantees for deterministic column sampling using ridge leverage scores. The matrix sketch returned by our algorithm is a column subset of the original matrix, yielding additional interpretability. Like the randomized counterparts, the deterministic algorithm provides $(1+\epsilon)$ error column subset selection, $(1+\epsilon)$ error projection-cost preservation, and an additive-multiplicative spectral bound. We also show that under the assumption of power-law decay of ridge leverage scores, this deterministic algorithm is provably as accurate as randomized algorithms. Lastly, ridge regression is frequently used to regularize ill-posed linear least-squares problems. While ridge regression provides shrinkage for the regression coefficients, many of the coefficients remain small but non-zero. Performing ridge regression with the matrix sketch returned by our algorithm and a particular regularization parameter forces coefficients to zero and has a provable $(1+\epsilon)$ bound on the statistical risk. As such, it is an interesting alternative to elastic net regularization.

Large Scale Stochastic Training of Neural Networks, Amir Gholaminejad (UC Berkeley)

The next milestone for machine learning is the ability to train on massively large datasets. The de facto method used for training neural networks is stochastic gradient descent, a sequential algorithm with poor convergence properties. One approach to address the challenge of large scale training, is to use large mini-batch sizes which allows parallel training. However, large batch size training often results in poor generalization performance. The exact reasons for this are still not completely understood, and all the methods proposed so far for resolving it (such as scaling learning rate or annealing batch size) are specific to a particular problem and do not generalize.
In the first part of the talk, I will show results analyzing large batch size training through the lens of the Hessian operator. The results rule out some of the common theories regarding large batch size training, such as problems with saddle points. In the second part, I will present our results on a novel Hessian based method in combination with robust optimization, that avoids many of the issues with first order methods such as stochastic gradient descent for large scale training.

Randomized Constrained Matrix Decompositions, Benjamin Erichson (University of Washington)

A wide range of phenomena in the physical, engineering, biological, and social sciences feature rich dynamics that give rise to multiscale structures in both space and time, including fluid dynamics, atmospheric-ocean interactions, climate modeling, epidemiology, and neuroscience. Constrained matrix factorizations are powerful techniques for modern data analysis, providing improved interpretation of low-rank structures by identifying localized spatial structures in the data and disambiguating between distinct time scales. However, the emergence of large-scale datasets has severely challenged our ability to analyze data using such techniques. We discuss randomized methods as a computational strategy to accelerate techniques such as sparse principal component analysis (SPCA) and nonnegative matrix factorization (NMF). The proposed algorithms are demonstrated using both synthetic and real world data, showing great computational efficiency and diagnostic performance.

Adventures with Randomized Algebra for Extreme-Scale Signal Processing, Anshumali Shrivastava (Rice University)

Sampling and Projection (or sketching) are the two fundamental hammers in Randomized Numerical Linear Algebra for reducing the size and scale of the problem at hand. At extreme scale, conventional sampling and projections themselves are prohibitively expensive.
In this talk, I will discuss some of my recent and surprising findings on the use of hashing algorithms for large-scale estimations. Locality Sensitive Hashing (LSH) is a hugely popular algorithm for sub-linear near neighbor search. However, it turns out that fundamentally LSH is a constant time (amortized) adaptive sampler from which efficient near-neighbor search is one of the many possibilities. LSH offers a unique capability to do smart sampling and statistical estimations at the cost of few hash lookups. Our observation bridges data structures (probabilistic hash tables) with efficient unbiased statistical estimations. I will demonstrate how this dynamic and efficient sampling beak the computational barriers in adaptive estimations where it is possible that we pay roughly the cost of uniform sampling but get the benefits of adaptive sampling. I will demonstrate the power of one simple idea for three favorite problems 1) Partition function estimation for large NLP models such as word2vec, 2) Adaptive Gradient Estimations for efficient SGD and 3) Sub-Linear Deep Learning with Huge Parameter Space.
In the end, if time permits, I will switch to memory cost show a simple hashing algorithm, which is a count-min sketch in disguise, can shrink memory requirements associated with k-class classification exponentially! Using our algorithms, we can train 100,000 classes with 400,000 features, on a single Titan X while only needing 5% or less memory required to store all the weights. Running a simple logistic regression on this data, the model size of 320GB is unavoidable.

Unbiased Estimates for Linear Regression via Volume Sampling, Michal Derezinski (UC Santa Cruz)

We study the following basic machine learning task: Given a fixed set of n input points in a d-dimensional linear regression problem, we wish to predict a hidden response value for each of the points. We can only afford to attain the responses for a small subset of the points that are then used to construct linear predictions for all points in the dataset. The performance of the predictions is evaluated by the total square loss on all responses. We show that a good approximate solution to this least squares problem can be obtained from just dimension d many responses by using a joint sampling technique called volume sampling. Moreover, the least squares solution obtained for the volume sampled subproblem is an unbiased estimator of optimal solution based on all n responses. This unbiasedness is a desirable property that is not shared by standard subset selection techniques.
Motivated by these basic properties, we develop a theoretical framework for studying volume sampling, which leads to a number of new expectation formulas and statistical guarantees that are of importance not only to least squares regression but also numerical linear algebra in general. Our methods lead to several extensions of volume sampling, including a regularized variant, and we propose the first efficient algorithms which make this technique a practical tool in the machine learning toolbox.

Smoothed Analysis of Low Rank Solutions to Semidefinite Programs via Burer Monteiro Factorization, Praneeth Netrapalli (Microsoft Research India)

Semidefinite programs (SDP) are important in learning and combinatorial optimization with numerous applications. In pursuit of low-rank solutions and low complexity algorithms, we consider the Burer--Monteiro factorization approach for solving SDPs. We show that all approximate local optima are global optima for the penalty formulation of appropriately rank-constrained SDPs as long as the number of constraints scales sub-quadratically with the desired rank of the optimal solution. Our result is based on a simple penalty function formulation of the rank-constrained SDP along with a smoothed analysis to avoid worst-case cost matrices.

Matrix-free Construction of HSS Representations Using Adaptive Randomized Sampling, Xiaoye S. Li (LBNL)

An active research area in recent years is the development of fast hierarchical matrix tools for linear and eigen solvers. Although the theoretical foundation for the hierarchical matrices has been solidified, there is a lack of robust algorithms and software that can handle many practical issues. For example, randomized sampling has been shown to be an effective tool to reveal the low rank structures, but choosing the right number of samples is difficult.
In this talk we present new results for HSS compression using an Adaptive Randomized Sampling strategy. In particular, we developed a robust stopping criterion based on a new stochastic relative error estimation. We present results for situations when the dense matrix is given and in the matrix-free setting. We show some practical difficulties about implementation and present some solutions that get around the problems.

Fast SVD in the Presence of Noise, Matan Gavish (Hebrew University of Jerusalem)

In the presence of measurement noise, the quality of fast randomized low-rank approximations deteriorates with noise level. Under suitable assumptions, this phenomenon can be quantified (as function of the noise level, sketch size and underlying matrix rank) and mitigated.

A Fast Algorithm for Computing the Maximum Weight Base in a Linear Matroid, Huy Nguyen (Northeastern University)

A fundamental algorithmic result for matroids is that the maximum weight base can be computed using the greedy algorithm. For linear matroids, an important question is the time complexity of computing such a base. In this work, we give a fast algorithm that computes the same output as the greedy algorithm for linear matroids.

Matrix Martingales in Randomized Numerical Linear Algebra, Rasmus Kyng (Yale University)

A matrix martingale is a sequence of random matrices where the expectation of each matrix in the sequence equals the preceding matrix, conditional on the earlier parts of the sequence. Concentration results for matrix martingales have become an important tool in the analysis of algorithms in randomized numerical linear algebra. Simple and fast algorithms for many well-studied problems can be analyzed in using martingales. We survey recent results on using matrix martingales for randomized constructions of sparse approximations of graphs and discuss in detail the use of matrix martingales for analyzing approximate Gaussian elimination on Laplacian matrices associated with undirected and directed graphs.

Fast Algorithms for Multivariate ODEs arising in Sampling and Learning, Santosh Vempala (Georgia Institute of Technology)

Sampling logconcave functions arising in statistics and machine learning has been a subject of intensive study. Recent developments include analyses for Langevin dynamics and Hamiltonian Monte Carlo (HMC). While both approaches have dimension-independent bounds for the underlying continuous processes under sufficiently strong smoothness conditions, the resulting discrete algorithms have complexity and number of function evaluations growing with the dimension. Here we give a nearly linear implementation of HMC for sampling from a broad class of densities, with the number of iterations and function evaluations being polylogarithmic in the dimension (rather than polynomial as in previous work). This class includes the widely-used loss function for logistic regression with incoherent weight matrices. Our main contribution is a fast solver for multivariate Ordinary Differential Equations whose solution is close to a low-degree polynomial. We establish logarithmic bounds on the degree for the differential equations arising in HMC. Joint work with Yin Tat Lee and Zhao Song.

Spectrally Robust Graph Isomorphism, Yiannis Koutis (New Jersey Institute of Technology)

We discuss two generalizations of the graph isomorphism problem:
(a) Spectral Dominance: On input of two PSD matrices A and B, does there exist a permutation matrix P such that P'*B*P is spectrally dominated by A?
(b) Spectrally Robust Isomorphism: On input of two PSD matrices A and B, and a constant k, does there exists a permutation matrix P such that the condition number of the pair (A,P'*B*P) is bounded above by k?
We show that Spectral Dominance is NP-hard, even when A and B are graph Laplacians. On the other hand, we show that Spectrally Robust Isomorphism is tractable when A and B are Laplacians of trees that have bounded degree. We also discuss several related open questions.
[The talk is based on joint work with A. Kolla, V. Madan and A. K. Sinop that appeared in ICALP '18.]

Subspace Clustering using Ensembles of K-Subspaces, Laura Balzano (University of Michigan)

We discuss a novel approach to the subspace clustering problem that leverages ensembles of the K-subspaces (KSS) algorithm with random initializations. We extend existing results in subspace clustering to show that correct clustering can be achieved by any algorithm that obtains (possibly perturbed) measurements of any monotonic function of the inner product between points -- so it is possible to cluster with missing data, compressed data, or in other scenarios where only an approximation of inner products is available. We then show that a single iteration of KSS with random initialization produces such a measurement, and hence our algorithm can provably recover subspaces under the same conditions as state-of-the-art algorithms. The finding is, to the best of our knowledge, the first recovery guarantee for evidence accumulation clustering and for KSS variants. It also provides insight into random initializations of subspace arrangements. We show on synthetic data that our method performs well in the traditionally challenging settings of subspaces with large intersection, subspaces with small principal angles, and noisy data. Finally, we show our algorithm achieves state-of-the-art performance across several benchmark datasets, including a resulting error for the COIL-20 database that is less than half that achieved by existing algorithms.

Join the CompressiveSensing subreddit or the Google+ Community or the Facebook page and post there !
Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.

CfP: Khipu 2019: Latin American Meeting in Artificial Intelligence, Montevideo, Uruguay, November 11-15th, 2019

Mauricio just sent me the following:

"Hi Igor,

I hope you are doing well. I'm contacting you to let you know about the first edition of Khipu: an annual LATAM meeting in AI that will be held in Facultad de Ingeniería (UdelaR), Montevideo, Uruguay, Nov. 11-15, 2019. The main goal of the event is to strengthen the AI local community by bringing high level training and by fostering research collaborations within and outside the region.

We'll have terrific speakers! Among the confirmed speakers is Yoshua Bengio (Turing award) and Jeff Dean (Google Senior Fellow). Full list of confirmed speakers is at https://khipu.ai.

We'd really appreciate it if you help us spread the announcement below so that we can reach as many people (in particular Latin American students/researchers) as possible!

Thanks a lot and congratulations on the blog. I'm a huge fan :)

best,
mauricio"

Thanks Mauricio ! Here is the announcement: 

**Khipu 2019: Latin American Meeting in Artificial Intelligence**
Call for participation (apologies for multiple copies)

Applications are now open for the first edition of Khipu: Latin American Meeting in Artificial Intelligence. The event aims to strengthen the local community by bringing high level training and by fostering research collaborations within and outside the region. Khipu 2019 will be held in Montevideo, Uruguay, in November 11-15th. The event will have a summer school component with lectures on different topics in machine learning paired with practical coding sessions, but it will also host research talks, round tables and moments where attendees from academia and industry will be able to share their work.
Confirmed speakers include this year’s Turing award Yoshua Bengio and Google Senior Fellow Jeff Dean. 

More information about application instructions and the full set of invited speakers are available at https://khipu.ai. Join our mailing list and/or follow us on twitter (@khipu_ai) and keep updated with our latest news.
Important Dates:

• March 29th 2019: Application open
• June 28th 2019: Application deadline
• August 2nd 2019: Acceptance notifications

We look forward to your participation!
Khipu organising committee.

Join the CompressiveSensing subreddit or the Google+ Community or the Facebook page and post there !

Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.