Hyperparameter Optimization: A Spectral Approach

From the introduction

In this paper we introduce a new spectral approach to hyperparameter optimization based on harmonic analysis of Boolean functions. At a high level, the idea is to fit a sparse polynomial function to the discrete, high-dimensional function mapping hyperparameters to loss, and then optimize the resulting sparse polynomial. Using ideas from discrete Fourier analysis and compressed sensing, we can give provable guarantees for a sparse-recovery algorithm that admits an efficient, paralellizable implementation. Here we are concerned with the tradeoff between running time and sample complexity for learning Boolean functions f where sampling uniformly from f is very expensive. This approach appears to be new and allows us to give uniform-distribution learning algorithms for Boolean concept classes such as decision trees that match the state-of-the-art in running time and save dramatically in sample complexity.

Hyperparameter Optimization: A Spectral Approach by Elad Hazan, Adam Klivans, Yang Yuan

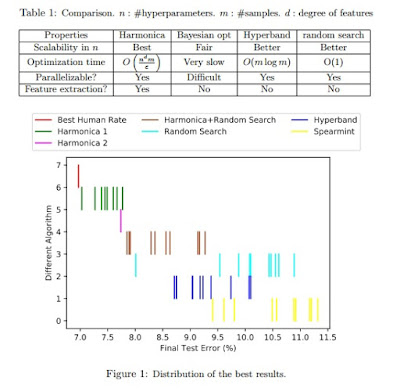
We give a simple, fast algorithm for hyperparameter optimization inspired by techniques from the analysis of Boolean functions. We focus on the high-dimensional regime where the canonical example is training a neural network with a large number of hyperparameters. The algorithm - an iterative application of compressed sensing techniques for orthogonal polynomials - requires only uniform sampling of the hyperparameters and is thus easily parallelizable. Experiments for training deep nets on Cifar-10 show that compared to state-of-the-art tools (e.g., Hyperband and Spearmint), our algorithm finds significantly improved solutions, in some cases matching what is attainable by hand-tuning. In terms of overall running time (i.e., time required to sample various settings of hyperparameters plus additional computation time), we are at least an order of magnitude faster than Hyperband and even more so compared to Bayesian Optimization. We also outperform Random Search 5X. Additionally, our method comes with provable guarantees and yields the first quasi-polynomial time algorithm for learning decision trees under the uniform distribution with polynomial sample complexity, the first improvement in over two decades.

h/t François on Twitter

Join the CompressiveSensing subreddit or the Google+ Community or the Facebook page and post there !

Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.