First, here is another example of inverse problems for electrical engineers investigated by Davood Shamsi, Petros Boufounos and Farinaz Koushanfar in Noninvasive Leakage Power Tomography of Integrated Circuits by Compressive Sensing. The abstract reads:
We introduce a new methodology for noninvasive post-silicon characterization of the unique static power profile (tomogram) of each manufactured chip. The total chip leakage is measured for multiple input vectors in a linear optimization framework where the unknowns are the gate leakage variations. We propose compressive sensing for fast extraction of the unknowns since the leakage tomogram contains correlations and can be sparsely represented. A key advantage of our approach is that it provides leakage variation estimates even for inaccessible gates. Experiments show that the methodology enables fast and accurate noninvasive extraction of leakage power characteristics.
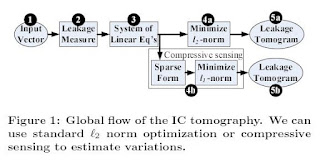
It looks as though one is mapping an electronics board onto an image map in order to "spariify" the model and then use Compressive Sensing to perform the equivalent of a group testing problem yielding a 30% improvement over an l2 based technique.
The second paper is another intriguing paper by John Wright and Yi Ma, who are some of the authors behind the face recognition technique using l1 minimization. Well, this time, they go further in a work that is likely to yield some penetrating results. As Yi Ma mentioned to me, they show that "... it is probably the first work showing L1 can actually deal with dense errors or signals..". If one of you thinks otherwise, please let the authors know.
 In Dense Error Correction via l1 Minimization, John Wright and Yi Ma introduce us to the following:
In Dense Error Correction via l1 Minimization, John Wright and Yi Ma introduce us to the following:This paper studies the problem of recovering a non-negative sparse signalfrom highly corrupted linear measurements
, where e is an unknown error vector whose nonzero entries may be unbounded. Motivated by an observation from face recognition in computer vision, this paper proves that for highly correlated (and possibly overcomplete) dictionaries A, any non-negative, sufficiently sparse signal x can be recovered by solving an l1-minimization problem:
min ||x||_1 + ||e||_1 subject to y = Ax + e
More precisely, if the fractionof errors is bounded away from one and the support of x grows sublinearly in the dimension m of the observation, then as m goes to infinity, the above l1-minimization succeeds for all signals x and almost all sign-and-support patterns of e. This result suggests that accurate recovery of sparse signals is possible and computationally feasible even with nearly 100% of the observations corrupted. The proof relies on a careful characterization of the faces of a convex polytope spanned together by the standard crosspolytope and a set of iid Gaussian vectors with nonzero mean and small variance, which we call the “cross and-bouquet” model. Simulations and experimental results corroborate the findings, and suggest extensions to the result.
No comments:
Post a Comment