A Generalized Least Squares Matrix Decomposition by Genevera Allen, Logan Grosenick, Jonathan Taylor. The abstract reads:
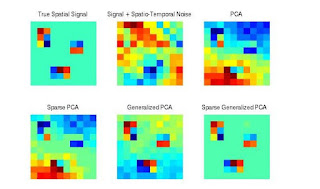
Variables in high-dimensional data sets common in neuroimaging, spatial statistics, time series and genomics often exhibit complex dependencies that can arise, for example, from spatial and/or temporal processes or latent network structures. Conventional multivariate analysis techniques often ignore these relationships. We propose a generalization of the singular value decomposition that is appropriate for transposable matrix data, or data in which neither the rows nor the columns can be considered independent instances. By nding the best low rank approximation of the data with respect to a transposable quadratic norm, our decomposition, entitled the Generalized least squares Matrix Decomposition (GMD), directly accounts for dependencies in the data. We also regularize the factors, introducing the Generalized Penalized Matrix Factorization (GPMF). We develop fast computational algorithms using the GMD to perform generalized PCA (GPCA) and the GPMF to perform sparse GPCA and functional GPCA on massive data sets. Through simulations we demonstrate the utility of the GMD and GPMF for dimension reduction, sparse and functional signal recovery, and feature selection with high-dimensional transposable data
Thanks Genevera.
No comments:
Post a Comment