Welcome to the Matrix Factorization Jungle

- Update: The Matrix Factorization Jungle Page is here , you are also welcome to join the Matrix Factorization Group on LinkedIn. -

While we are beginning to see some good solvers out of the generic compressed sensing reconstruction solver front or let's call them sparse recovery solvers, a similar chaotic front is now appearing in front of our eyes in terms of Matrix Factorization. The discovery that the nuclear norm could serve as a proxy to the rank functional has led to a slew of different approaches that encompass older formulation like the PCA. Initially, one of the emphasis was to decrease the computational time to approximate the rank through the use of random projection and concentration of measure results as embodied in the Randomized PCA. But with functionals approximating the rank, we began to see other use of these concentration results stemming from the high dimensionality of our current data deluge . I am surely missing out on some approaches but here are the two schools of thoughts I have seen so far. On the one hand, we have folks looking to perform matrix decomposition such as:

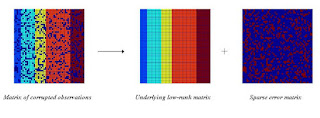
A = L + S + N

where L is a low rank approximation, S is a sparse matrix of potentially large coefficients and N a "noisy matrix". This problem is called Principal Component Pursuit and it's little sister A = L + S is called Robust PCA. Many of these approaches tend to aim for solving the matrix completion issue that the Netflix problem was trying to solve. Beyond the camera surveillance problem, the rise of Facebook, LinkedIn and other some such players is invariably pushing for these "privacy interpolating" approaches. There are a number of issues with these decomposition, including whether or not the sparse components can themselves be considered low or high rank for instance. But I am sure the subject will be beaten to death and improved over time. 

Then there is the second school of thoughts around folks coming from a background of statistics who somehow want to perform Dictionary learning and Sparse Principal Component Analysis. Here we have:

M = U V^T

As one can see in this presentation slide, the L + S decomposition is also somehow included in this approach.

What I find fascinating here is that this train of thought eventually leads to defining new norms in order to expand on the whole structured sparsity concept. But as in any jungle, Sparse PCA, for instance does not even seem to have a unique definition (see expository slide: Methods for Sparse PCA by Daniela Witten)

If you want to learn more about this new jungle of opportunity, you may want to check the following excellent resources:

• Matrix recovery algorithms of Stephen Becker's outstanding repository.
• Francis Bach and Julien Mairal sets of presentations and the attendant SPAMs software
• Low-Rank Matrix Recovery and Completion via Convex Optimization site of Arvind Ganesh.
• Nuclear Norm and Matrix Recovery through SDP by Christoph Helmberg

Liked this entry ? subscribe to the Nuit Blanche feed, there's more where that came from