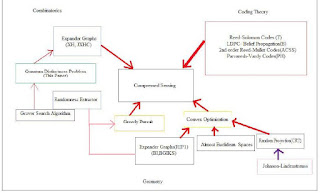
Efficient Compressed Sensing using Lossless Expander Graphs with Fast Bilateral Quantum Recovery Algorithm by Sina Jafarpour. The abstract reads:
Compressed Sensing is a novel approach to bypass the Nyquist sampling limits whenever the signals are sparse, and to compress them simultaneously. In this paper, improving our previous results, we will propose a compressed sensing algorithm based on the high-quality lossless unbalanced vertex expander graphs, with a fast and simple quantum decoding algorithm. Exploiting the unique neighborhood property of the lossless expander graphs in combination with the efficient quantum algorithm for finding distinct elements among a set we will prove the validity and efficiency of the algorithm and will show how the combination of the lossless expander graphs and quantum recovery algorithm leads to a general compressed sensing framework which is as good as the previous results in terms of the sketch size, encoding time, update time, and having explicit construction; furthermore, it is superior to the previous recovery algorithms in both the recovery time and simplicity of implementation. Finally we will show how the algorithm can be modified to be robust for a well-structured family of almost sparse signals. The robust algorithm will first find the position of the largest elements of the signal, and then using this information finds efficiently an explicit sparse approximation for the original signal.

According to Sina's website, we are going to see more on that idea with "Quantum Computers can make Compressed Sensing Faster" a paper under preparation.
No comments:
Post a Comment