Dan let us know that some folks back in Ireland (There is no 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem by Gary McGuire, Bastian Tugemann, Gilles Civario) have found that if you give 16 clues in a Sudoku's problem then, there is probably more than one solution to it. With 17 clues, then there is only one solution. They seem to have gone through an exhaustive search to find that result.
The reason I mention this today is because I wonder what the generic Donoho-Tanner phase transition can bring to the table. Let us remember that the Sudoku problem was set up as the recovery of a solution to an underdetermined linear system of equations (Linear Systems, Sparse Solutions, and Sudoku by Prabhu Babu, Kristiaan Pelckmans, Petre Stoica, and Jian Li, implementation in Python available thanks to Ben Moran), i.e. a typical instance of compressive sensing. The problem was then solved using a reweighted L1 approach but it looks like there are problem that cannot be solved with it. Since then, Gabriel Peyre and Yue Lu made another version of that solver and have a numerical tour discussing a matlab implementation.
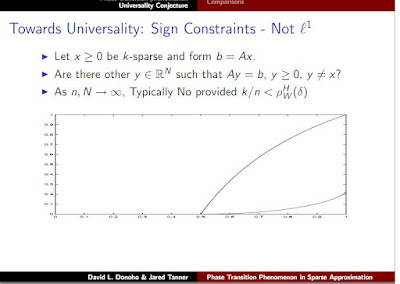
If I recall correctly, the Donoho-Tanner phase transition shows that (see Jared Tanner's presentation at Texas A&M in 2008) under a specific curve, there was only one sparse solution to these underdetermined systems of linear equations (see Precise Undersampling Theorems for a more in-depth look)
I haven't had time to look back at the set up of the Sudoku problem as an underdetermined system of linear equations or if the solution has to be positive but I wonder where this 16/17 result recently found through brute force fit in this diagram. Do you know ?
Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.
No comments:
Post a Comment