How does the Rice one pixel camera work ?

I have had this question asked several times by colleagues and friends, so I decided to use my talent in Microsoft Paint to explain it.

The problem: If you have only one sensitive pixel/photodetector/radiation detector/Teraherz detector and you want to take a 10 MP image, what do you do ? Let us also imagine you also have access to a chip built with 10 million mirrors (Texas Instrument DMD) and you can command each of these tiny 15 microns by 15 microns mirrors. Each can be switched to shine on your detector or not.

First option (the raster mode):
You switch all your mirrors but one away from your detector. You do that once

twice (with another pixel)

thrice (with yet another pixel)
four times (....)
five times (...)
....5 millions times (...)
until you reach the last 10 millionth pixel.
You now have ten million information which put together provides you with a 10 MP image. You then use a small processor to perform the Discrete Cosine Transform which eventually provides you with a JPEG image.

Second option (the Compressive Sensing mode):

You tell the DMD to display a set of random tilings of shining and none shining mirrors.

You do that once with an initial random tiling, this is your first CS measurement

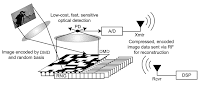then you do this again with a second random tiling,  this is your second CS measurement

then you do this again with a third random tiling,  this is your third CS measurement
and so on.

Compressed sensing tells you that with very high probability, you will get the same result as the raster mode  above but with much fewer CS measurements Instead of taking 10 million raster mode measurements , you are likely to need 20 percent CS measurements, maybe even less.

The idea is that most natural images are sparse in bases ranging from cosines, wavelets to curvelets (this is why JPEG does a tremendous job in decreasing the size of most images). Functions that represent random tiling of reflective and non reflective mirrors (0s and 1s) are incoherent with these basis.. Hence, the second method consists in taking projection of an image of interest on this random basis.


The advantages of the second option are:

1. the overall sensor requires very low power because there is no CPU/GPU/FPGA trying to do compression like JPEG.
2. the sensor is dedicated to acquiring information. Information processing can be done somewhere else ( think on some other planet)
   
3. compared to raw images, the information to be transmitted is very much compressed albeit not optimally.
4. you can spend all your money designing the very best sensitive pixel you want, it may even act as a spectrometer (looking at many different energy bands), radiation detector and so forth.

Terry Tao provides a much clearer explanation albeit with no images. All information about this system can be found at Rice.