CS: Multiplicative Noise Effect on the Donoho-Tanner Phase Transition (Part 4)

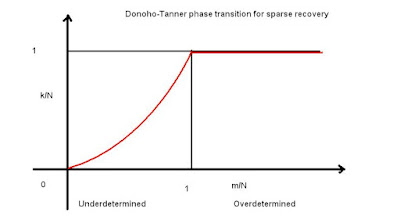
The Donoho-Tanner phase transition for sparse recovery is being shown below with the y-axis as k/N instead of traditional k/m variable.

Instead of using the least square solver like we need on our previous installment, we now try to see the effect of multiplicative noise on the Donoho-Tanner phase transition with SL0. The figure above shows the noiseless case (i.e. no multiplicative noise). We use the SL0 solver that solves the basis pursuit problem, i.e.

min||x||_1 st Ax = b

Yes, this is not an ideal problem but we will look at the result of a LASSO solver in our next installment. In the meantime, here is the result for epsilon = 1/1000 or 0.1%

Since we have some noise, we could use the cross and bouquet trick, i.e solve using [A I] instead of [A] in the reconstruction stage.

So, we begin to see that the noise is beginning to destroy the DT phase transition in the underdetermined regime but that using the cross and bouquet trick that destruction is shifted in the overdetermined regime leaving the underdetermined part of the transition barely untouched. Here at m/N =1, we have k/N close to 0.6 instead of 1 in the noiseless case.

What about epsilon = 3/1000 or 0.3% ? Here are the figures for the simple and the cross and bouquet cases.

 Even in the cross and bouquet case,  at m/N =1, the phase transition peaks at k/N =0.3 for m/N = 1. For epsilon = 5/1000 or 0.5%, we obtain the following figures:

One note that for the overdetermined side, over a certain threshold, we continue on having a solution irrespective of sparsity. Let us also note that in the underdetermined case, a small sparsity level can allow some recovery unlike the least square case.

Next installment with a LASSO solver.