- This post has been updated, see discussion with Phil Schniter after the bonus section -
In a LinkedIn thread, it was mentioned that problems with 0/1 signals might be a niche market. With the improvements due to Moore's law, those markets might become less niche. Three cases in point,
In short, we are beginning to see hardware that stops recording after the first photon. In some of these instances, it is not a traditional 1-bit compressive sensing approach or if it is, it is implemented at the hardware level. To get an understanding of how compressive sensing could help those new technologies, I am going to focus on the QIS technology currently developed by Eric Fossum ( Saturday Morning Video: CMOS Image Sensors: Tech Transfer from Saturn to your Cell Phone) and featured in some of his presentations. The following images are slides excerpts from:
- Quanta Image Sensor (QIS) – Possible paradigm shift for the future
- Quanta Image Sensor (QIS): Early Research Progress
(for those who don't know Eric Fossum is the man behind the use of CMOS in all cameras). I am adding comment underneath each slide:
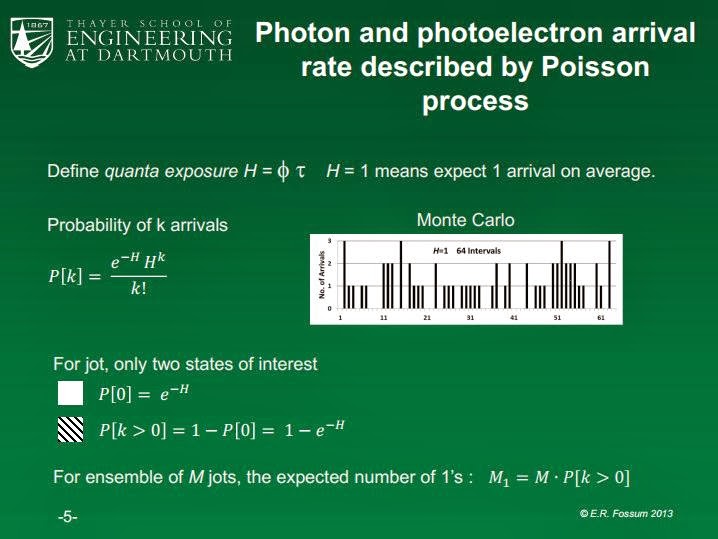
The figure on the right tells me that each frame is sparse.
The reason, each frame is sparse compared to the current CMOS technology is because you need 4220 jots (QIS pixel) to be equivalent to current CMOS pixel.
The back end description shows the possibility of performing some sorts of processing and multiplexing which I see as a way to perform some sort of convolution i.e. matrix vector multiply.
what is interesting here is that each jot frame could be assembled in some nonlinear fashion to produce a new type of image (instead of just summing them)
One can definitely imagine new kinds of imaging based on that technology. More on that later.
One bit is the beginning and end of this technology, for now.
Ah, the fun challenge of getting 5Tb/s off the chip! As one can see compressive sensing is just one way of performing some sorts of compression. The reason it was mentioned for QIS is because jot frames are sparse, made up of 0s and 1s and the fact that the compression is simply a matrix vector multiply (i.e. it is a non adaptive process and it is lossless). Let us also note that the 1s are not the result of a quantization operation. Quite simply, in order to operate a compression of this dataset, the following operation y = A x must be undertaken with x is vectorized binary bit plane (jot frame, bernouilli vector), A is a matrix and y is the resulting compressed version of x. Compressive sensing comes into play with the choice of the right A and because of the sparse nature of x.
getting into the detail of things
This is the most interesting figure. For starters, let's get a correspondence between terms used in QIS and those used in CS:
- M1 in QIS is k (sparsity) in CS,
- M in QIS is N (embedding dimension) in CS, it is the size of vector x defined earlier
- Bit density D in QIS is sparsity rate k/N in CS, and finally
- m is number of measurements needed to have lossless compression with a CS approach, it is the size of vector y defined earlier.
Note: ideally m is (much) less than M (QIS) or N in (CS).
What does compressive sensing bring to QIS ?
- Depending on how A is chosen, using a compressive sensing approach, m could be order of O(M1log(M/M1)) ( resp. O(klog(N/k)) ) all the way down to M1 + 1 (resp. k + 1), see below for further information on how to do this.
- By taking one measurement and summing all the bits of the jot frame/bit plane, one knows directly the sparsity of the scene. This is important as one can taylor the size of A for each bit plane/jot frame.
Let us consider that A is a Bernouilli Gaussian matrix (I suggested Bernouilli in 2011 -see above_ but I was wrong, the signal x is bernouilli while the measurement matrix has to have zero-mean ) [ Thanks Phil Schniter for the correction ]
Matrix A is a Bernouilli Gaussian matrix
If one reads the paper Expectation-Maximization Gaussian-Mixture Approximate Message Passing by Jeremy P. Vila, and Philip Schniter (code is EM-GM-AMP: An Algorithm for Sparse Reconstruction)
x axis is m/N (CS) or m/M (QIS)
y axis is k/m (CS) or M1/m (QIS)
A is of size m x N
In order to estimate the size of A, one needs to evaluate m given a specific bit density D (k/m*m/N) and M1 (k sparsity) from the figure above. m can be found at the intersection between the hyperbole D and the curve showing the phase diagram shown above (we are only interested in the phase diagram curve of EM-GM-AMP-MOS, below that curve reconstruction is always possible, above it, reconstruction of x from x is not possible). For instance if D = 0.1, then k/m*m/N = 0.1, or about m/N =0.25 and k/m=0.37. It means that the possibility of recovering the exact x (jot frame/bit plane) for 1000 (N) jots means that one needs at least m = 250 rows for A and that one can only recover up to M1 or k = 92 bits. If one wants to recover vector with a higher number of bits; one then needs to increase the number of measurements.
One should note that if D = 0.5 or above, the phase diagram ( phase diagram curve of EM-GM-AMP-MOS ) shows that k = m is the limit. In other words, the number of measurements is the same as the sparsity of the jot field. In effect the problem is also symmetric, when the zeros take the place of the ones, sparsity number climbs above 50% and the solution being sought is the reverse of a solution below 50%. Let us note that the solver EM-GM-AMP-MOS respect that symmetry and can solve this problem sparsity above 50%. This is noteworthy as the solver can do this without being told anything about the signal beforehand. Let us note that other solvers cannot do this.
If D is less than 0.5 can we do better than the computation shown above. Can you have a number of measurements close to the sparsity level of the jot field ? The answer is yes but one need to craft A in a specific manner.
Matrix A is a Hadamard Seeded Matrix
The news came out in a stunning development in breaking the Donoho-Tanner phase transition ? in the paper entitled Statistical physics-based reconstruction in compressed sensing by Florent Krzakala, Marc Mézard, François Sausset, Yifan Sun, Lenka Zdeborová, there is a phase diagram as follows:
This type of very interesting result come from a specific construction for A. More recently in Compressed sensing and Approximate Message Passing with spatially-coupled Fourier and Hadamard matrices by Jean Barbier, Florent Krzakala, Christophe Schülke ( implementation is here and the attendant code http://aspics.krzakala.org/ ), that construction was extended to a Hadamard style measurement matrix with -1/0/1 coefficients. Let us also note that the matrix is also sparse as shown in the figure below:
In that new construction, one should expect m = k + 1, a result similar to the previous Bernouilli construction but for D less than 0.5.
In other words, a compression scheme for QIS could use either a Bernouilli (first scenario) or a seeded matrix architecture (second scenario) that yields:
- a lossless compression scheme
- a linear compression scheme
- a very efficient reconstruction scheme as both reconstruction solvers used above are AMP style; meaning that they require few matrix-vector multiply to reconstruct x from y.
Both solvers are readily available from their respective authors as listed above.
Bonus:
Bonus:
- Let us note the other interesting aspect of this compression scheme is that increasing the frame rate does not translate into a change in data handling architecture. If the framerate is increased by 10 or 100 fold, the sparsity is the jot frame is also on average divided by 10 or a 100, yet the number of compressed measured remain the same. The only showstopper is not the bandwidth but the ability to perform the matrix-vector multiply.
- One could also contemplate working with compressed measurement directly to perform detection work.
-Update 1-
Following the initial writing of this blog entry, I had a back and forth discussion with Phil Schniter on the subject. Here is what he had to say on competing ways to compress the information coming from the bit planes especially for high throughput data (5Tb/s):
"...I think a traditional (non-CS) coding scheme would work better at those rates. One big advantage, as I see it, is that they keep all of the arithmetic *binary*, i.e., they work in a Galois field instead of the Real (or Complex) field. Note that in CS, even if you build a Hadamard matrix and have a Bernoulli signal vector, you are working with integers and not bits on the acquisition side, and with real numbers on the sparse reconstruction side. Bits are much simpler!
Something else to consider is whether you want to place the computational burden on the coder or the decoder. As we know, in CS, the burden is on the decoder whereas in traditional coding the burden is on the encoder. I would guess that there are traditional source-coding schemes that trade coding efficiency for encoding complexity (which might be advantageous for QIS), but really this is outside my expertise.Another question is whether some sort of group-testing would be appropriate, but perhaps the bit-plane data is not sparse enough...."
Clearly, if we have low exposure (low light or high frame rate), then bit density (D) or sparsity could be made lower. One would have to see how some of the group testing solution fare.
Other interesting slides include:
the QIS curves looks like old photography curves.
interesting comparison with multi-bit systems.
Sparse field of rain drops, it looks like a more advanced means of knowing the weather than the 2bit Aggie Weather station.












2 comments:
I have not properly read up on the QIS principle, but the photon counting approach you explain makes me wonder if this work on Poisson compressed sensing could be relevant to it:
http://people.ee.duke.edu/~willett/papers/PCS.pdf
http://people.ee.duke.edu/maxim/pubs/raginsky_willett_harmany_marcia_TSP10.pdf
(An anonymous reviewer of a paper of mine was kind enough to point those references out to me in another context.)
I also notice another detail: there seems to be a non-linear function involved in the measuring in that the detectors simply seem to count *one or more* photons, so any positive number of photons is truncated (quantized) to one. I am not sure if this matters, though, as you seem to suggest that these measured detections are themselves the sparse data one would hope to reconstruct from fewer measurements through compressed sensing.
Finally, I just noticed this paper http://www.sciencemag.org/content/343/6166/58 which sounds somewhat related. I have only read the abstract so far.
Thanks Thomas.
Yes the Poisson noise will be there but it is part of the measurement process so there is nothing that can be done about it.
As regards to the nonlinear detection, in the QIS itself it is only one photon being counted, there is the possibility of being nonlinear but it is not contemplated in the QIS work if I understand correctly.
Igor
Post a Comment