Nuit Blanche: Compressive Sensing This Week

Wednesday, April 25, 2012

Compressive Sensing This Week

Through the Google Summer of Code 2012, Sergey Lisitsyn will port SLEP to Shogun ( A Large Scale Machine Learning Toolbox). SHOGUN is implemented in C++ and interfaces to Matlab(tm), R, Octave and Python.

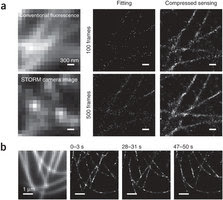
The following paper just appeared in Nature: Faster STORM using compressed sensing by Lei Zhu, Wei Zhang, Daniel Elnatan & Bo Huang. The abstract reads:\

In super-resolution microscopy methods based on single-molecule switching, the rate of accumulating single-molecule activation events often limits the time resolution. Here we developed a sparse-signal recovery technique using compressed sensing to analyze images with highly overlapping fluorescent spots. This method allows an activated fluorophore density an order of magnitude higher than what conventional single-molecule fitting methods can handle. Using this method, we demonstrated imaging microtubule dynamics in living cells with a time resolution of 3 s.

Hardware-Efﬁcient Random Sampling of Fourier-Sparse Signals by Patrick Maechler, Norbert Felber, and Hubert Kaeslin, Andreas Burg. The abstract reads:

Spectrum sensing, i.e. the identiﬁcation of occupied frequencies within a large bandwidth, requires complex sampling hardware. Measurements suggest that only a small fraction of the available spectrum is actually used at any time and place, which allows a sparse characterization of the frequency domain signal. Compressed sensing (CS) can exploit this sparsity and simplify measurements. We investigate the performance of a very simple hardware architecture based on the slope analogto-digital converter (ADC), which allows to sample signals at unevenly spaced points in time. CS algorithms are used to identify the occupied frequencies, which can be continuously distributed across a large bandwidth.

Emily Allstot let me know of her paper: Compressed Sensing System Considerations for ECG and EMG Wireless Biosensors by Dixon, A. M. R. , Allstot, E. G. ; Gangopadhyay, D. ; Allstot, D. J. . The abstract reads:

Compressed sensing (CS) is an emerging signal processing paradigm that enables sub-Nyquist processing of sparse signals such as electrocardiogram (ECG) and electromyogram (EMG) biosignals. Consequently, it can be applied to biosignal acquisition systems to reduce the data rate to realize ultra-low-power performance. CS is compared to conventional and adaptive sampling techniques and several system-level design considerations are presented for CS acquisition systems including sparsity and compression limits, thresholding techniques, encoder bit-precision requirements, and signal recovery algorithms. Simulation studies show that compression factors greater than 16X are achievable for ECG and EMG signals with signal-to-quantization noise ratios greater than 60 dB.

Here is a good news-bad news story:

The bad news? testing RIP is tougher than deciding P vs NP (see paper below).
The good news? we don't care about RIP.

Certifying the restricted isometry property is hard by Afonso S. Bandeira, Edgar Dobriban, Dustin G. Mixon, William F. Sawin. The abstract reads:

This paper is concerned with an important matrix condition in compressed sensing known as the restricted isometry property (RIP). We demonstrate that testing whether a matrix satisfies RIP is hard for NP under randomized polynomial-time reductions. Our reduction is from the NP-complete clique decision problem, and it uses ideas from matroid theory. As a consequence of our result, it is impossible to efficiently test for RIP provided NP \not\subseteq BPP, an assumption which is slightly stronger than P \neq NP.

Robust Computation of Linear Models, or How To Find a Needle in a Haystack by Gilad Lerman, Michael McCoy, Joel Tropp, AND Teng Zhang . The abstract reads:

Abstract. Consider a dataset of vector-valued observations that consists of a modest number of noisy inliers, which are explained well by a low-dimensional subspace, along with a large number of outliers, which have no linear structure. This work describes a convex optimization problem, called reaper, that can reliably t a low-dimensional model to this type of data. The paper provides an effi cient algorithm for solving the reaper problem, and it documents numerical experiments which con rm that reaper can dependably nd linear structure in synthetic and natural data. In addition, when the inliers are contained in a low-dimensional subspace, there is a rigorous theory that describes when reaper can recover the subspace exactly.

Analysis and Design of Irregular Graphs for Node-Based Verification-Based Recovery Algorithms in Compressed Sensing by Yaser Eftekhari, Amir H. Banihashemi, Ioannis Lambadaris. The abstract reads:

In this paper, we present a probabilistic analysis of iterative node-based verification-based (NB-VB) recovery algorithms over irregular graphs in the context of compressed sensing. Verification-based algorithms are particularly interesting due to their low complexity (linear in the signal dimension $n$). The analysis predicts the average fraction of unverified signal elements at each iteration $\ell$ where the average is taken over the ensembles of input signals and sensing matrices. The analysis is asymptotic ($n \rightarrow \infty$) and is similar in nature to the well-known density evolution technique commonly used to analyze iterative decoding algorithms. Compared to the existing technique for the analysis of NB-VB algorithms, which is based on numerically solving a large system of coupled differential equations, the proposed method is much simpler and more accurate. This allows us to design irregular sensing graphs for such recovery algorithms. The designed irregular graphs outperform the corresponding regular graphs substantially. For example, for the same recovery complexity per iteration, we design irregular graphs that can recover up to about 40% more non-zero signal elements compared to the regular graphs. Simulation results are also provided which demonstrate that the proposed asymptotic analysis matches the performance of recovery algorithms for large but finite values of $n$.

Fusion of Matching Pursuits for Compressed Sensing Signal Reconstruction by Sooraj K. Ambat, Saikat Chatterjee, K.V.S. Hari . The abstract reads:

Matching Pursuits are very popular in Compressed Sensing for sparse signal recovery. Though many of the Matching Pursuits possess elegant theoretical guarantees for performance, it is well known that their performance depends on the statistical distribution of the non-zero elements in the sparse signal. In practice, the distribution of the sparse signal may not be known {\em a priori}. It is also observed that performance of Matching Pursuits degrades as the number of available measurements decreases from a threshold value which is method dependent. To improve the performance in these situations, we introduce a novel fusion framework for Matching Pursuits and also propose two algorithms for sparse recovery. Through Monte Carlo simulations we show that the proposed schemes improve sparse signal recovery in clean as well as noisy measurement cases.

Estimating Unknown Sparsity in Compressed Sensing by Miles E. Lopes. The abstract reads:

Within the framework of compressed sensing, many theoretical guarantees for signal reconstruction require that the number of linear measurements $n$ exceed the sparsity ||x||_0 of the unknown signal x\in\R^p. However, if the sparsity ||x||_0 is unknown, the choice of $n$ remains problematic. This paper considers the problem of estimating the unknown degree of sparsity of $x$ with only a small number of linear measurements. Although we show that estimation of ||x||_0 is generally intractable in this framework, we consider an alternative measure of sparsity s(x):=\frac{\|x\|_1^2}{\|x\|_2^2}, which is a sharp lower bound on ||x||_0, and is more amenable to estimation. When $x$ is a non-negative vector, we propose a computationally efficient estimator \hat{s}(x), and use non-asymptotic methods to bound the relative error of \hat{s}(x) in terms of a finite number of measurements. Remarkably, the quality of estimation is \emph{dimension-free}, which ensures that \hat{s}(x) is well-suited to the high-dimensional regime where n<

Fast thresholding algorithms with feedbacks for sparse signal recovery by Tiebin Mi, Shidong Li, Yulong Liu. The abstract reads:

We provide another framework of iterative algorithms based on thresholding, feedback and null space tuning for sparse signal recovery arising in sparse representations and compressed sensing. Several thresholding algorithms with various feedbacks are derived, which are seen as exceedingly effective and fast. Convergence results are also provided. The core algorithm is shown to converge in finite many steps under a (preconditioned) restricted isometry condition. Numerical studies about the effectiveness and the speed of the algorithms are also presented. The algorithms are seen as particularly effective for large scale problems.

Technical Report: Observability of a Linear System under Sparsity Constraints by Wei Dai, Serdar Yüksel. The abstract reads:

Consider an n−dimensional linear system where it is known that there are at most k less than n non-zero components in the initial state. The observability problem, that is the recovery of the initial state, for such a system is considered. We obtain sufﬁcient conditions on the number of the available observations to be able to recover the initial state exactly for such a system. Both deterministic and stochastic setups are considered for system dynamics. In the former setting, the system matrices are known deterministically, whereas in the latter setting, all of the matrices are picked from a randomized class of matrices. The main message is that, one does not need to obtain full n observations to be able to uniquely identify the initial state of the linear system, even when the observations are picked randomly, when the initial condition is known to be sparse.

Adaptive Restart for Accelerated Gradient Schemes by Brendan O'Donoghue, Emmanuel Candes. The abstract reads:

In this paper we demonstrate a simple heuristic adaptive restart technique that can dramatically improve the convergence rate of accelerated gradient schemes. The analysis of the technique relies on the observation that these schemes exhibit two modes of behavior depending on how much momentum is applied. In what we refer to as the 'high momentum' regime the iterates generated by an accelerated gradient scheme exhibit a periodic behavior, where the period is proportional to the square root of the local condition number of the objective function. This suggests a restart technique whereby we reset the momentum whenever we observe periodic behavior. We provide analysis to show that in many cases adaptively restarting allows us to recover the optimal rate of convergence with no prior knowledge of function parameters.

Analysis of Sparse Representations Using Bi-Orthogonal Dictionaries by Mikko Vehkaperä, Yoshiyuki Kabashima, Saikat Chatterjee, Erik Aurell, Mikael Skoglund, Lars Rasmussen. The abstract reads:

The sparse representation problem of recovering an N dimensional sparse vector x from M < N linear observations y = Dx given dictionary D is considered. The standard approach is to let the elements of the dictionary be independent and identically distributed (IID) zero-mean Gaussian and minimize the l1-norm of x under the constraint y = Dx. In this paper, the performance of l1-reconstruction is analyzed, when the dictionary is bi-orthogonal D = [O1 O2], where O1,O2 are independent and drawn uniformly according to the Haar measure on the group of orthogonal M x M matrices. By an application of the replica method, we show that the typical compression threshold for such D is the same as for the IID Gaussian dictionary.

Fast and Robust Parametric Estimation of Jointly Sparse Channels by Y. Barbotin, M. Vetterli . The abstract reads:

We consider the joint estimation of multipath channels obtained with a set of receiving antennas and uniformly probed in the frequency domain. This scenario fits most of the modern outdoor communication protocols for mobile access or digital broadcasting among others.

Such channels verify a Sparse Common Support property (SCS) which was used in a previous paper to propose a Finite Rate of Innovation (FRI) based sampling and estimation algorithm. In this contribution we improve the robustness and computational complexity aspects of this algorithm. The method is based on projection in Krylov subspaces to improve complexity and a new criterion called the Partial Effective Rank (PER) to estimate the level of sparsity to gain robustness.

If P antennas measure a K-multipath channel with N uniformly sampled measurements per channel, the algorithm possesses an O(KPNlogN) complexity and an O(KPN) memory footprint instead of O(PN^3) and O(PN^2) for the direct implementation, making it suitable for K << N. The sparsity is estimated online based on the PER, and the algorithm therefore has a sense of introspection being able to relinquish sparsity if it is lacking. The estimation performances are tested on field measurements with synthetic AWGN, and the proposed algorithm outperforms non-sparse reconstruction in the medium to low SNR range (< 0dB), increasing the rate of successful symbol decodings by 1/10th in average, and 1/3rd in the best case. The experiments also show that the algorithm does not perform worse than a non-sparse estimation algorithm in non-sparse operating conditions, since it may fall-back to it if the PER criterion does not detect a sufficient level of sparsity.

The algorithm is also tested against a method assuming a "discrete" sparsity model as in Compressed Sensing (CS). The conducted test indicates a trade-off between speed and accuracy.