We experimentally demonstrate a photon-counting, single-pixel, laser radar camera for 3D imaging where transverse spatial resolution is obtained through compressive sensing without scanning. We use this technique to image through partially obscuring objects, such as camouflage netting. Our implementation improves upon pixel-array based designs with a compact, resource-efficient design and highly scalable resolution.
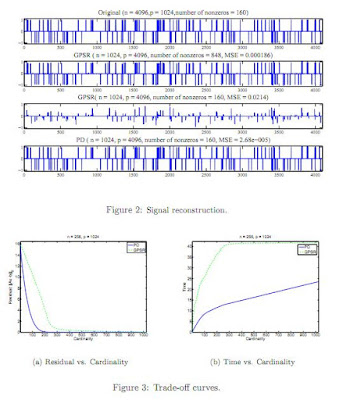
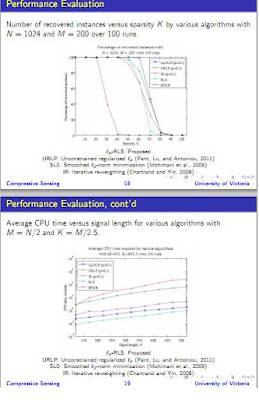
Recovery of Sparse Signals from Noisy Measurements Using an l`p-Regularized Least-Squares Algorithm by J. K. Pant,
Wu-Sheng. Lu, and
Andrea Antoniou.
What I note from this presentation is that
SL0, a very simple code, provides very similar capabilities and is much faster than this reweighted lp solver.
Not related to CS per se, but I found the presentation by one of the author of this paper intriguing, in part because it would seem to me that CS should be all over this field:
In them, there is a talk about a 2pi/3 period which introduces well the next paper:
Spectral Compressive Sensing by
Marco Duarte,
Richard Baraniuk. The abstract reads:
Compressive sensing (CS) is a new approach to simultaneous sensing and compression of sparse and compressible signals based on randomized dimensionality reduction. To recover a
signal from its compressive measurements, standard CS algorithms seek the sparsest signal in some discrete basis or frame that agrees with the measurements. A great many applications feature smooth or modulated signals that are frequency sparse and can be modeled as a superposition of a small number of sinusoids. Unfortunately, such signals are only sparse in the discrete Fourier transform (DFT) domain when the sinusoid frequencies live precisely at the center of the DFT bins; when this is not the case, CS recovery performance degrades signi�cantly. In this paper, we introduce the spectral CS (SCS) recovery framework for arbitrary frequency sparse signals. The key ingredients are an over-sampled DFT frame, a signal model that inhibits closely spaced sinusoids, and classical sinusoid parameter estimation algorithms from the �eld of spectral estimation. Using periodogram and line spectral estimation methods (speci�cally Thomson's multitaper method and MUSIC), we demonstrate that SCS signi�cantly outperforms current state-of-the-art CS algorithms based on the DFT while providing provable bounds on the number of measurements required for stable recovery
In di�ffusion MRI (dMRI) domain, many High Angular Resolution Di�usion Imaging (HARDI) methods were proposed to estimate Ensemble Average Propagator (EAP) and Orientation Distribution Function (ODF). They normally need many samples, which limits their applications. Some Compressive Sensing (CS) based methods were proposed to estimate ODF in Q-Ball Imaging (QBI) from limited samples. However EAP estimation is much more difficult than ODF in QBI. Recently Spherical Polar Fourier Imaging (SPFI) was proposed to represent di�usion signal using Spherical Polar Fourier (SPF) basis without specific assumption on di�ffusion signals and analytically obtain EAP and ODF via the Fourier dual SPF (dSPF) basis from arbitrarily sampled signal. Normally the coe�cients of SPF basis are estimated via Least Square with weighted `2 norm regularization (`2-SPFI). However, `2-SPFI needs a truncated basis to avoid overfitting, which brings some estimation errors. By considering the Fourier relationship between EAP and signal and the Fourier basis pair provided in SPFI, we propose a novel EAP estimation method, named `1-SPFI, to estimate EAP from limited samples using CS technique, and favorably compare it to the classical `2-SPFI method. `1-SPFI estimates the coe�cients in SPFI using least square with weighted `1 norm regularization. The weights are designed to enhance the sparsity. `1-SPFI significantly accelerates the ordinary CS based Fourier reconstruction method. This is performed by using SPF basis pair in CS estimation process which avoids the numerical Fourier transform in each iteration step. By considering high order basis in `1 optimization, `1-SPFI improves EAP reconstruction especially for the angular resolution. The proposed `1-SPFI was validated by synthetic, phantom and real data. The CS EAP and ODF estimations are discussed in detail and we show that recovering the angular information from CS EAP requires much less samples than exact CS EAP reconstruction. Various experiments on synthetic, phantom and real data validate the fact that SPF basis can sparsely represent DW-MRI signals and `1-SPFI largely improves the CS EAP reconstruction especially the angular resolution.
Since Diffusion Tensor Imaging (DTI) cannot detect the fiber crossing, many new works beyond DTI has been proposed to explore the q-space. Most works, known as single shell High Angular Resolution Imaging (sHARDI), focus on single shell sampling and reconstruct the Orientation Distribution Function (ODF). The ODF, which has no radial information at all, is just one of features of Ensemble Average Propagator (EAP). Diffusion Spectrum Imaging (DSI) is a standard method to estimate EAP via numerical Fourier Transform (FT), which needs lots of samples and is impractical for clinical study. Spherical Polar Fourier Imaging (SPFI) [1,2] was proposed to represent the signal using SPF basis, then the EAP and the ODF have analytical closed forms. So the estimation of the coefficients under SPF basis is very important. In [1,2], the coefficients are estimated based on a standard Least Square (LS) with L2 norm regularization (L2-L2). In this paper, we propose to estimate the coefficients using LS with L1 norm regularization (L2-L1), also named as Least Absolute Selection and Shrinkage Operator (LASSO). And we prove that the L2-L1 estimation of the coefficients is actually the well known Compressive Sensing (CS) method to estimate EAP, which brings lots of Mathematical tools and possibility to improve the sampling scheme in q-space
Compressive sampling is a well-known approach to reconstruct sparse signals based on a limited number of measurements. In spectrum sensing applications for cognitive radio though, only reconstruction of the power spectrum of the signal is required, instead of the signal itself. In this paper, we present a new method for power spectrum reconstruction based on samples produced by a sub-Nyquist rate sampling device. The stationary assumption on the received analog signal causes the measurements at the output of the compressive sampling block to be cyclo-stationary, or the measurement vectors to be stationary. We investigate the relationship between the autocorrelation matrix of the measurement vectors and that of the received analog signal, which we represent by its Nyquist rate sampled version. Based on this relationship, we are able to express the autocorrelation sequence of the received wide sense stationary signal as a linear function of the vectorized autocorrelation matrix of the measurement vectors. Depending on the compression rate, we can present the problem as either over-determined or under-determined. Our focus will be mainly on the over-determined case, in which the reconstruction does not require any additional constraints. Two types of sampling matrices are examined, namely complex Gaussian and multi-coset sampling matrices. For both of them, we can derive conditions under which the over-determined system will result in a unique solution for the power spectrum by adopting a simple least squares (LS) algorithm. In the case of multi-coset sampling, further improvement on the quality of the power spectrum estimates can be attained by optimizing the condition of the sampling matrix.
Sparse estimation methods are aimed at using or obtaining parsimonious representations of data or models. They were first dedicated to linear variable selection but numerous extensions have now emerged such as structured sparsity or kernel selection. It turns out that many of the related estimation problems can be cast as convex optimization problems by regularizing the empirical risk with appropriate non-smooth norms. The goal of this paper is to present from a general perspective optimization tools and techniques dedicated to such sparsity-inducing penalties. We cover proximal methods, block-coordinate descent, reweighted ℓ2-penalized techniques, working-set and homotopy methods, as well as nonconvex formulations and extensions, and provide an extensive set of experiments to compare various algorithms from a computational point of view.
Separation-based Joint Decoding in Compressive Sensing by Hsieh-Chung Chen and H. T. Kung. The abstract reads:
Abstract—
We introduce a joint decoding method for compressive sensing that can simultaneously exploit sparsity of individual components of a composite signal. Our method can significantly reduce the total number of variables decoded jointly by separating variables of large magnitudes in one domain and using only these variables to represent the domain. Furthermore, we enhance the separation accuracy by using joint decoding across multiple domains iteratively. This separation-based approach improves the decoding time and quality of the recovered signal. We demonstrate these benefits analytically and by presenting empirical results.
Identifying Bad Measurements in Compressive Sensing by
H.T. Kung,
Tsung-Han Lin,
Dario Vlah. The abstract reads:
We consider the problem of identifying bad measurements in compressive sensing. These bad measurements can be present due to malicious attacks and system malfunction. Since the system of linear equations in compressive sensing is underconstrained, errors introduced by these bad measurements can result in large changes in decoded solutions. We describe methods for identifying bad measurements so that they can be removed before decoding. In a new separation-based method we separate out top nonzero variables by ranking, eliminate the remaining variables from the system of equations, and then solve the reduced overconstrained problem to identify bad measurements. Comparing to prior methods based on direct or joint ℓ1-minimization, the separation-based method can work under a much smaller number of measurements. In analyzing the method we introduce the notion of inversions which governs the separability of large nonzero variables.
CloudSense: Continuous Fine-Grain Cloud Monitoring With Compressive Sensing by
H.T. Kung,
Chit-Kwan Lin and
Dario Vlah. The abstract reads:
Continuous fine-grain status monitoring of a cloud data center enables rapid response to anomalies, but handling the resulting torrent of data poses a significant challenge. As a solution, we propose CloudSense, a new switch design that performs in-network compression of status streams via compressive sensing. Using MapReduce straggler detection as an example of cloud monitoring, we give evidence that CloudSense allows earlier detection of stragglers, since finer-grain status can be reported for a given bandwidth budget. Furthermore, CloudSense showcases the advantage of an intrinsic property of compressive sensing decoding that enables detection of the slowest stragglers first. Finally, CloudSense achieves in-network compression via a low-complexity encoding scheme, which is easy and convenient to implement in a switch. We envision that CloudSense switches could form the foundation of a “compressed status information plane” that is useful for monitoring not only the cloud data center itself, but also the user applications that it hosts.
Partitioned Compressive Sensing with Neighbor-Weighted Decoding by
H.T. Kung and
Stephen J. Tarsa. The abstract reads:
Compressive sensing has gained momentum in recent years as an exciting new theory in signal processing with several useful applications. It states that signals known to have a sparse representation may be encoded and later reconstructed using a small number of measurements, approximately proportional to the signal’s sparsity rather than its size. This paper addresses a critical problem that arises when scaling compressive sensing to signals of large length: that the time required for decoding becomes prohibitively long, and that decoding is not easily parallelized. We describe a method for partitioned compressive sensing, by which we divide a large signal into smaller blocks that may be decoded in parallel. However, since this process requires a significant increase in the number of measurements needed for exact signal reconstruction, we focus on mitigating artifacts that arise due to partitioning in approximately reconstructed signals. Given an error-prone partitioned decoding, we use large magnitude components that are detected with highest accuracy to influence the decoding of neighboring blocks, and call this approach neighbor-weighted decoding. We show that, for applications with a predefined error threshold, our method can be used in conjunction with partitioned compressive sensing to improve decoding speed, requiring fewer additional measurements than unweighted or locally-weighted decoding.
Collaborative Compressive Spectrum Sensing in a UAV Environment by
Hsieh-Chung Chen,
H. T. Kung, ,
Dario Vlah, Daniel Hague,
Michael Muccio and Brendon Poland. The abstract reads:
Spectrum sensing is of fundamental importance to many wireless applications including cognitive radio channel assignment and radiolocation. However, conventional spectrum sensing can be prohibitively expensive in computation and network bandwidth when the bands under scanning are wide and highly contested. In this paper we propose distributed spectrum sensing with multiple sensing nodes in a UAV environment. The ground nodes in our scheme sense the spectrum in parallel using compressive sensing. Each sensor node transmits compressive measurements to a nearby UAV in the air. The UAV performs decoding on the received measurements; it decodes information with increasing resolution as it receives more measurements. Furthermore, by a property of compressive sensing decoding, frequencies of large magnitude responses are recovered first. In the proposed scheme, as soon as the UAV detects the presence of such high-power frequencies from a sensor, this information is used to aid decoding for other sensors. We argue that such collaboration enabled by UAV will greatly enhance the decoding accuracy of compressive sensing. We use packet-loss traces acquired in UAV flight experiments in the field, as well as field experiments involving software-defined radios, to validate the effectiveness of this distributed compressive sensing approach
Measurement Combining and Progressive Reconstruction in Compressive Sensing by
Hsieh-Chung Chen,
H. T. Kung,
Dario Vlah, Bruce Suter. The abstract reads:
Compressive sensing has emerged as an important new technique in signal acquisition due to the surprising property that a sparse signal can be captured from measurements obtained at a sub-Nyquist rate. The decoding cost of compressive sensing, however, grows superlinearly with the problem size. In distributed sensor systems, the aggregate amount of compressive measurements encoded by the sensors can be substantial, and the decode cost for all the variables involved can be large. In this paper we propose a method to combine measurements from distributed sensors. With our method we can transport and store a single combined measurement set, rather than multiple sets for all sensors. We show that via source separation and joint decoding, it is possible to recover an approximate to the original signal from combined measurements using progressive reconstruction which focuses on individual sensors. This results in a reduction in the number of variables used in decoding and consequently a reduced decoding time. We show that the computed approximation to the signal can still have sufficient accuracy for target detection. We describe the combining approach and the associated progressive reconstruction, and we illustrate them with image recovery for simple target detection examples.

by
Arian Maleki, Laura Anitori, Zai Yang,
Richard Baraniuk. The abstract reads:
Recovering a sparse signal from an undersampled set of random linear measurements is the main problem of interest in compressed sensing. In this paper, we consider the case where both the signal and the measurements are complex. We study the popular reconstruction method of $\ell_1$-regularized least squares or LASSO. While several studies have shown that the LASSO algorithm offers desirable solutions under certain conditions, the precise asymptotic performance of this algorithm in the complex setting is not yet known. In this paper, we extend the approximate message passing (AMP) algorithm to the complex signals and measurements and obtain the complex approximate message passing algorithm (CAMP). We then generalize the state evolution framework recently introduced for the analysis of AMP, to the complex setting. Using the state evolution, we derive accurate formulas for the phase transition and noise sensitivity of both LASSO and CAMP.
Sparse Recovery with Graph Constraints: Fundamental Limits and Measurement Construction by
Meng Wang,
Weiyu Xu,
Enrique Mallada,
Ao Tang. The abstract reads:
This paper addresses the problem of sparse recovery with graph constraints in the sense that we can take additive measurements over nodes only if they induce a connected subgraph. We provide explicit measurement constructions for several special graphs. A general measurement construction algorithm is also proposed and evaluated. For any given graph $G$ with $n$ nodes, we derive order optimal upper bounds of the minimum number of measurements needed to recover any $k$-sparse vector over $G$ ($M^G_{k,n}$). Our study suggests that $M^G_{k,n}$ may serve as a graph connectivity metric.
Sparsity without the Complexity: Loss Localisation using Tree Measurements by
Vijay Arya,
Darryl Veitch. The abstract reads:
We study network loss tomography based on observing average loss rates over a set of paths forming a tree -- an ill-conditioned linear problem for the link loss probabilities. We examine in detail the role of sparsity as a regularising principle, pointing out that the problem is technically distinct from others in the compressed sensing literature. We exploit the tree structure to derive sufficient conditions for sparse solutions to be unique, and present a fast single-pass linear algorithm which outputs the minimal $\ell_1$ solution, which we prove is always unique, and always has the minimal $\ell_0$ (sparsity). By considering the placement of lossy links within the tree, we show that sparse solutions remain unique much more often than is commonly supposed. We prove similar results for a noisy version of the problem.
Advanced phase retrieval: maximum likelihood technique with sparse regularization of phase and amplitude by
Artem Migukin,
Vladimir Katkovnik,
Jaakko Astola. The abstract reads:
Sparse modeling is one of the efficient techniques for imaging that allows recovering lost information. In this paper, we present a novel iterative phase-retrieval algorithm using a sparse representation of the object amplitude and phase. The algorithm is derived in terms of a constrained maximum likelihood, where the wave field reconstruction is performed using a number of noisy intensity-only observations with a zero-mean additive Gaussian noise. The developed algorithm enables the optimal solution for the object wave field reconstruction. Our goal is an improvement of the reconstruction quality with respect to the conventional algorithms. Sparse regularization results in advanced reconstruction accuracy, and numerical simulations demonstrate significant enhancement of imaging.
Structured Sparsity and Generalization by
Andreas Maurer,
Massimiliano Pontil. The abstract reads:
We present a data dependent generalization bound for a large class of regularized algorithms which implement structured sparsity constraints. The bound can be applied to standard squared-norm regularization, the lasso, the group lasso, some versions of the group lasso with overlapping groups, multiple kernel learning and other regularization schemes. In all these cases competitive results are obtained. A novel feature of our bound is that it can be applied in an infinite dimensional setting such as the lasso in a separable Hilbert space or multiple kernel learning with a countable number of kernels.
Exact Reconstruction Conditions for Regularized Modified Basis Pursuit by
Wei Lu,
Namrata Vaswani. The abstract reads:
In this correspondence, we obtain exact recovery conditions for regularized modified basis pursuit (reg-mod-BP) and discuss when the obtained conditions are weaker than those for modified-CS or for basis pursuit (BP). The discussion is also supported by simulation comparisons. Reg-mod-BP provides a solution to the sparse recovery problem when both an erroneous estimate of the signal's support, denoted by $T$, and an erroneous estimate of the signal values on $T$ are available.
Symmetric Group Testing and Superimposed Codes by
Amin Emad, Jun Shen,
Olgica Milenkovic. The abstract reads:
We describe a generalization of the group testing problem termed symmetric group testing. Unlike in classical binary group testing, the roles played by the input symbols zero and one are "symmetric" while the outputs are drawn from a ternary alphabet. Using an information-theoretic approach, we derive sufficient and necessary conditions for the number of tests required for noise-free and noisy reconstructions. Furthermore, we extend the notion of disjunct (zero-false-drop) and separable (uniquely decipherable) codes to the case of symmetric group testing. For the new family of codes, we derive bounds on their size based on probabilistic methods, and provide construction methods based on coding theoretic ideas.
Differential Phase-contrast Interior Tomography by
Wenxiang Cong,
Ge Wang. The abstract reads:
Differential phase contrast interior tomography allows for reconstruction of a refractive index distribution over a region of interest (ROI) for visualization and analysis of internal structures inside a large biological specimen. In this imaging mode, x-ray beams target the ROI with a narrow beam aperture, offering more imaging flexibility at less ionizing radiation. Inspired by recently developed compressive sensing theory, in numerical analysis framework, we prove that exact interior reconstruction can be achieved on an ROI via the total variation minimization from truncated differential projection data through the ROI, assuming a piecewise constant distribution of the refractive index in the ROI. Then, we develop an iterative algorithm for the interior reconstruction and perform numerical simulation experiments to demonstrate the feasibility of our proposed approach.
.
Recovering compressively sampled signals using partial support information by
Michael P. Friedlander,
Hassan Mansour,
Rayan Saab,
Ozgur Yilmaz. The abstract reads:
We study recovery conditions of weighted !1 minimization for signal reconstruction from compressed sensing measurements when partial support information is available. We show that if at least 50% of the (partial) support information is accurate, then weighted !1 minimization is stable and robust under weaker sufficient conditions than the analogous conditions for standard !1 minimization. Moreover, weighted !1 minimization provides better upper bounds on the reconstruction error in terms of the measurement noise and the compressibility of the signal to be recovered. We illustrate our results with extensive numerical experiments on synthetic data and real audio and video signals.
Several presentation from
Felix J. Herrmann's group:
- Tristan van Leeuwen, Felix J. Herrmann. Probing the extended image volume for seismic velocity inversion.
- Tristan van Leeuwen. A correlation-based misfit criterion for wave-equation traveltime tomography.
- Tristan van Leeuwen, Mark Schmidt, Michael P. Friedlander, Felix J. Herrmann. A hybrid stochastic-deterministic method for waveform inversion.
- Aleksandr Aravkin, Tristan van Leeuwen, James Burke, Felix J. Herrmann. Sparsity promoting formulations and algorithms for FWI.
- Felix J. Herrmann,Aleksandr Aravkin, Tristan van Leeuwen, Xiang Li. FWI with sparse recovery: a convex-composite approach.
- Aleksandr Aravkin, Tristan van Leeuwen, Felix J. Herrmann. Robust FWI using Student's t-distribution.
- Felix J. Herrmann. Lecture 2. Gene Golub SIAM Summer School July 4 - 15, 2011.
By the way, this use of the Student's t-distribution is something I have heard about on sparse approximation from
Aleks Jakulin a while back on
Andrew's
Statistical Modeling, Causal Inference, and Social Science blog. Of related interest is
the mention of Andrew's
paper back in 1992.
Convex Approaches to Model Wavelet Sparsity Patterns by
Nikhil S. Rao,
Robert D. Nowak,
Stephen J. Wright,
Nick G. Kingsbury. The abstract reads
Statistical dependencies among wavelet coefficients are commonly represented by graphical models such as hidden Markov trees (HMTs). However, in linear inverse problems such as deconvolution, tomography, and compressed sensing, the presence of a sensing or observation matrix produces a linear mixing of the simple Markovian dependency structure. This leads to reconstruction problems that are non-convex optimizations. Past work has dealt with this issue by resorting to greedy or suboptimal iterative reconstruction methods. In this paper, we propose new modeling approaches based on group-sparsity penalties that leads to convex optimizations that can be solved exactly and efficiently. We show that the methods we develop perform significantly better in deconvolution and compressed sensing applications, while being as computationally efficient as standard coefficient-wise approaches such as lasso.
And finally, we have a list of abstracts only::
One-step-ahead Kinematic Compressive Sensing by Hover F., R. Hummel, U. Mitra, and G. Sukhatme. The abstract reads:
A large portion of work on compressive sampling and sensing has focused on reconstructions from a given measurement set. When the individual samples are expensive and optional, as is the case with autonomous agents operating in a physical domain and under specic energy limits, the CS problem takes on a new aspect because the projection is column-sparse, and the number of samples is not necessarily large. As a result, random sampling may no longer be the best tactic. The underlying incoherence properties in ℓ0 reconstruction, however, can still motivate the purposeful design of samples in planning for CS with one or more agents; we develop here a greedy and computationally tractable sampling rule that will improve errors relative to random points. Several example cases illustrate that the approach is e�ective and robust.
Accelerated diffusion spectrum imaging in the human brain using compressed sensing by Marion I. Menzel1,*, Ek T. Tan2, Kedar Khare2, Jonathan I. Sperl1, Kevin F. King3, Xiaodong Tao2, Christopher J. Hardy2, Luca Marinelli2. The abstract reads:
We developed a novel method to accelerate diffusion spectrum imaging using compressed sensing. The method can be applied to either reduce acquisition time of diffusion spectrum imaging acquisition without losing critical information or to improve the resolution in diffusion space without increasing scan time. Unlike parallel imaging, compressed sensing can be applied to reconstruct a sub-Nyquist sampled dataset in domains other than the spatial one. Simulations of fiber crossings in 2D and 3D were performed to systematically evaluate the effect of compressed sensing reconstruction with different types of undersampling patterns (random, gaussian, Poisson disk) and different acceleration factors on radial and axial diffusion information. Experiments in brains of healthy volunteers were performed, where diffusion space was undersampled with different sampling patterns and reconstructed using compressed sensing. Essential information on diffusion properties, such as orientation distribution function, diffusion coefficient, and kurtosis is preserved up to an acceleration factor of R = 4.
A compressed sensing-based iterative algorithm for CT reconstruction and its possible application to phase contrast imaging by Li X, Luo S. The abstract reads:
Computed Tomography (CT) is a technology that obtains the tomogram of the observed objects. In real-world applications, especially the biomedical applications, lower radiation dose have been constantly pursued. To shorten scanning time and reduce radiation dose, one can decrease X-ray exposure time at each projection view or decrease the number of projections. Until quite recently, the traditional filtered back projection (FBP) method has been commonly exploited in CT image reconstruction. Applying the FBP method requires using a large amount of projection data. Especially when the exposure speed is limited by the mechanical characteristic of the imaging facilities, using FBP method may prolong scanning time and cumulate with a high dose of radiation consequently damaging the biological specimens.
Fast Approximate Text Document Clustering Using Compressive Sampling by Laurence A. F. Park. The abstract reads:
Document clustering involves repetitive scanning of a document set, therefore as the size of the set increases, the time required for the clustering task increases and may even become impossible due to computational constraints. Compressive sampling is a feature sampling technique that allows us to perfectly reconstruct a vector from a small number of samples, provided that the vector is sparse in some known domain. In this article, we apply the theory behind compressive sampling to the document clustering problem using k-means clustering. We provide a method of computing high accuracy clusters in a fraction of the time it would have taken by directly clustering the documents. This is performed by using the Discrete Fourier Transform and the Discrete Cosine Transform. We provide empirical results showing that compressive sampling provides a 14 times increase in speed with little reduction in accuracy on 7,095 documents, and we also provide a very accurate clustering of a 231,219 document set, providing 20 times increase in speed when compared to performing k-means clustering on the document set. This shows that compressive clustering is a very useful tool that can be used to quickly compute approximate clusters.
Applying Compressive Sampling Theory Successfully to a Wideband Cooperative Spectrum Sensing Scheme by Duan Jiaqi,Li Yong
The introduction of the full paper reviews Refs.1 through 6 and then proposes the research of this paper,which is explained in sections 1,2,and 3.Their core is: " In the ideal cognitive radio(CR) systems,CR users are capable of sensing wide band spectrum simultaneously.However,due to the physical limits of front end devices,the real time entire spectrum sensing is difficult to be actualized.In order to tackle this problem,we propose a wide band spectrum sensing approach based on compressive sampling theory.First,we design a centralized multi-user parallel compressive sampling framework which realizes the high speed analog signal sampling of wide band spectrum sensing through low speed AD equipped CR users.Moreover,according to the compressive sampling theory,the proposed approach sufficiently utilizes the sparsity of primary signal on frequency domain.Thus,the base station can recover the frequency domain information of primary user by far less samples than Nyquist rate.Finally,the spectrum occupancy status can be determined by the recovery information." The simulation results,presented in Figs.3 and 4,reveal preliminarily that:(1) the proposed method has the higher detection probability and shorter sensing time than energy detection;(2) it needs only 10% memory units compared to conventional sensing schemes.
 Liked this entry ? subscribe to the Nuit Blanche feed, there's more where that came from
Liked this entry ? subscribe to the Nuit Blanche feed, there's more where that came from