A Numerical Exploration of Compressed Sampling Recovery by Charles Dossal , Gabriel Peyré and Jalal Fadili. The abstract reads:
This paper explores numerically the efficiency of L1 minimization for the recovery of sparse signals from compressed sampling measurements in the noiseless case. This numerical exploration is driven by a new greedy pursuit algorithm that computes sparse vectors that are difficult to recover by L1 minimization. The supports of these pathological vectors are also used to select sub-matrices that are ill-conditionned. This allows us to challenge theoretical identifiability criteria based on polytopes analysis and on restricted isometry conditions. We evaluate numerically the theoretical analysis without resorting to Monte-Carlo sampling, which tends to avoid worst case scenarios.and of related interest: Challenging Restricted Isometry Constants with Greedy Pursuit by Charles Dossal , Gabriel Peyré and Jalal Fadili. The abstract reads:
This paper proposes greedy numerical schemes to compute lower bounds of the restricted isometry constants that are central in compressed sensing theory. Matrices with small restricted isometry constants enable stable recovery from a small set of random linear measurements. We challenge this compressed sampling recovery using greedy pursuit algorithms that detect ill-conditionned sub-matrices. It turns out that these sub-matrices have large isometry constants and hinder the performance of compressed sensing recovery.
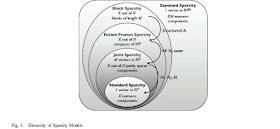
Sparse representations have emerged as a powerful tool in signal and information processing, culminated by the success of new acquisition and processing techniques such as Compressed Sensing (CS). Fusion frames are very rich new signal representation methods that use collections of subspaces instead of vectors to represent signals. This work combines these exciting fields to introduce a new sparsity model for fusion frames. Signals that are sparse under the new model can be compressively sampled and uniquely reconstructed in ways similar to sparse signals using standard CS. The combination provides a promising new set of mathematical tools and signal models useful in a variety of applications. With the new model, a sparse signal has energy in very few of the subspaces of the fusion frame, although it does not need to be sparse within each of the subspaces it occupies. This sparsity model is captured using a mixed l1/l2 norm for fusion frames.
A signal sparse in a fusion frame can be sampled using very few random projections and exactly reconstructed using a convex optimization that minimizes this mixed l1/l2 norm. The provided sampling conditions generalize coherence and RIP conditions used in standard CS theory. It is demonstrated that they are sufficient to guarantee sparse recovery of any signal sparse in our model. Moreover, an average case analysis is provided using a probability model on the sparse signal that shows that under very mild conditions the probability of recovery failure decays exponentially with increasing dimension of the subspaces.
In the reference section, I note the following lecture notes of Alexander Barvinok entitled Measure concentration.
I also found the following on the interwebs:
The sparse nature of location finding makes it desirable to exploit the theory of compressive sensing for indoor localization. In this paper, we propose a received signal strength (RSS)-based localization scheme in Wireless Local Area Networks (WLANs) using the theory of compressive sensing (CS), which offers accurate recovery of sparse signals from a small number of measurements by solving an ℓ1-minimization problem. In order to mitigate the effects of RSS variations due to channel impediments and mobile device orientation, a two-step localization scheme is proposed by exploiting affinity propagation for coarse localization followed by a CS-based fine localization to further improve the accuracy. We implement the localization algorithm on a WiFi-integrated mobile device to evaluate the performance. Experimental results indicate that the proposed system leads to substantial improvements on localization accuracy and complexity over the widely used traditional fingerprinting methods.
Compressive Sensing Based Positioning Using RSS of WLAN Access Points by Chen Feng, Wain Sy Anthea Au, Shahrokh Valaee, and Zhenhui Tan. The abstract reads:
The sparse nature of location finding problem makes the theory of compressive sensing desirable for indoor positioning in Wireless Local Area Networks (WLANs). In this paper, we address the received signal strength (RSS)-based localization problem in WLANs using the theory of compressive sensing (CS), which offers accurate recovery of sparse signals from a small number of measurements by solving an ℓ1-minimization problem. A pre-processing procedure of orthogonalization is used to induce incoherence needed in the CS theory. In order to mitigate the effects of RSS variations due to channel impediments, the proposed positioning system consists of two steps: coarse localization by exploiting affinity propagation, and fine localization by the CS theory. In the fine localization stage, access point selection problem is studied to further increase the accuracy. We implement the positioning system on a WiFi-integrated mobile device (HP iPAQ hx4700 with Windows Mobile 2003 Pocket PC) to evaluate the performance. Experimental results indicate that the proposed system leads to substantial improvements on localization accuracy and complexity over the widely used traditional fingerprinting methods.
In this paper we look at the problem of accurately reconstructing distributed signals through the collection of a small number of samples at a data gathering point. The techniques that we exploit to do so are Compressive Sensing (CS) and Principal Component Analysis (PCA). PCA is used to find transformations that sparsify the signal, which are required for CS to retrieve, with good approximation, the original signal from a small number of samples. Our approach dynamically adapts to non-stationary real world signals through the online estimation of their correlation properties in space and time; these are then exploited by PCA to derive the transformations for CS. The approach is tunable and robust, independent of the specific routing protocol in use and able to substantially outperform standard data collection schemes. The effectiveness of our recovery algorithm, in terms of number of transmissions in the network vs reconstruction error, is demonstrated for synthetic as well as for real world signals which we gathered from an actual wireless sensor network (WSN) deployment.We stress that our solution is not limited toWSNs but it can be readily applied to other types of network infrastructures that require the online approximation of large and distributed data sets.
Compressive Sensing (CS) has developed as an enticing alternative to the traditional process of signal acquisition. For a length-N signal with sparsity K, merely M = O(K logN) \lt\lt N random linear projections (measurements) can be used for robust reconstruction in polynomial time. Sparsity is a powerful and simple signal model; yet, richer models that impose additional structure on the sparse nonzeros of a signal have been studied theoretically and empirically from the CS perspective. In this work, we introduce and study a sparse signal model for streams of pulses, i.e., S-sparse signals convolved with an unknown F-sparse impulse response. Our contributions are threefold: (i) we geometrically model this set of signals as an infinite union of subspaces; (ii) we derive a sufficient number of random measurements M required to preserve the metric information of this set. In particular this number is linear merely in the number of degrees of freedom of the signal S + F, and sublinear in the sparsity K = SF; (iii) we develop an algorithm that performs recovery of the signal from M measurements and analyze its performance under noise and model mismatch. Numerical experiments on synthetic and real data demonstrate the utility of our proposed theory and algorithm. Our method is amenable to diverse applications such as the high resolution sampling of neuronal recordings and ultrawideband (UWB) signals.
and finally, On Local Dimension Estimation and Its Applications by Kevin Carter, Raviv Raich, and Alfred Hero, The abstract reads:
In this paper, we present multiple novel applications for local intrinsic dimension estimation. There has been much work done on estimating the global dimension of a data set, typically for the purposes of dimensionality reduction. We show that by estimating dimension locally, we are able to extend the uses of dimension estimation to many applications, which are not possible with global dimension estimation. Additionally, we show that local dimension estimation can be used to obtain a better global dimension estimate, alleviating the negative bias that is common to all known dimension estimation algorithms. We illustrate local dimension estimation’s uses towards additional applications, such as learning on statistical manifolds, network anomaly detection, clustering, and image segmentation.
A Graduate Summer School announcement on “Image Processing” at the Institute for Advanced Study (IAS),/Park City Mathematics Program (PCMI). APPLICATION DEADLINE JANUARY 31, 2010.
The program features the following course titles and descriptions:
The 2010 Summer Session in “Image Processing” will consist of eight graduate level lecture series. On any day during the summer session, three lectures will be offered. Graduate students are asked to attend the lectures as well as two daily problem sessions associated with the lecture and led by a graduate TA.
Richard Baraniuk, Rice University
Compressive Sensing: Sparsity-Based Signal Acquisition and Processing
Sensors, imaging systems, and communication networks are under increasing pressure to accommodate ever larger and higher-dimensional data sets; ever faster capture, sampling, and processing rates; ever lower power consumption; communication over ever more difficult channels; and radically new sensing modalities. The foundation of today’s digital data acquisition systems is the Shannon/Nyquist sampling theorem, which asserts that to avoid losing information when digitizing a signal or image, one must sample at least two times faster than the signal’s bandwidth, at the so-called Nyquist rate. Unfortunately, the physical limitations of current sensing systems combined with inherently high Nyquist rates impose a performance brick wall to a large class of important and emerging applications.
This lecture will overview some of the recent progress on compressive sensing, a new approach to data acquisition in which analog signals are digitized not via uniform sampling but via measurements using more general, even random, test functions. In stark contrast with conventional wisdom, the new theory asserts that one can combine “sub-Nyquist-rate sampling” with digital computational power for efficient and accurate signal acquisition. The implications of compressive sensing are promising for many applications and enable the design of new kinds of analog-to-digital converters; radio receivers, communication systems, and networks; cameras and imaging systems, and sensor networks.
Antonin Chambolle, École Polytechnique
Total-Variation based image reconstruction.
In the introduction we will recall the reason for which the Total Variation (TV) was introduced as a powerful tool for image recovery. The focus of the first lectures will be mostly on theoretical aspects. The definition and essential properties of the TV will be detailed, variational problems involving the related perimeter functional will also be considered. Then, we will study the “Rudin-Osher-Fatemi” problem (from a convex analysis point of view, the proximal operator associated to the TV). We will try to analyse some interesting properties of the solutions, including regularity issues.
A second part of the lectures will address algorithmic issues and describe the standard and less standard numerical methods for solving efficiently TV-like problems. In a last lecture, we will discuss original extensions which involve TV-like functionals.
Michael Elad, Israel Institute of Technology
Sparse & Redundant Representations – From Theory to Applications in Image Processing
Modeling natural image content is key in image processing. Armed with a proper model, one can handle various tasks such as denoising, restoration, separation, interpolation and extrapolation, compression, sampling, analysis and synthesis, detection, recognition, and more. Indeed, a careful study of the image processing literature reveals that there is an evolution of such models and their use in applications.
This short-course is all about one such model, which I call Sparse-Land for brevity. This specific model is intriguing and fascinating because of the beauty of its theoretical foundations, the superior performance it leads to in various applications, its universality and flexibility in serving various data sources, and its unified view, which makes all the above processing tasks clear and simple. In this course we shall starts with the mathematical foundations of this model, and then turn to present several image processing applications, where it is shown to lead to state-of-the-art results.
Selim Esedoglu, University of Michigan
Numerical methods for problems involving interfaces in imaging and vision.
We will discuss numerical methods for solving a number of interfacial problems that arise in image processing and computer vision applications. The applications we focus on will include image segmentation, image inpainting, as well as some inverse problems. Mathematical models for these typically involve an unknown curve in 2D or a surface in 3D. The numerical methods we discuss will include not only phase field, level sets, and threshold dynamics, but also certain globally optimal methods that convert non-convex optimization problems over curves and surfaces to convex optimization problems, which can then be solved to find the global minimum in a guaranteed fashion.
Anna Gilbert, University of Michigan
A survey of sparse approximation
The past 10 years have seen a confluence of research in sparse approximation amongst computer science, mathematics, and electrical engineering. Sparse approximation encompasses a large number of mathematical, algorithmic, and signal processing problems which all attempt to balance the size of a (linear) representation of data and the fidelity of that representation. I will discuss several of the basic algorithmic problems and their solutions, including connections to streaming algorithms and compressive sensing.
Yann LeCun, New York University
Learning Image Feature
Image recognition systems have traditionally consisted of a hard-wired feature extractor, followed by a trainable supervised classifier. One could argue that the next challenge of computer vision, machine learning, and image processing, is to devise methods that can automatically learn the feature extractor from labeled and unlabeled data. a particularly relevant task for image recognition is the so-called “Deep Learning” problem, whose object is to learn hierarchies of features with multiple levels of abstraction, and suitable invariances.
I will discuss the foundations of unsupervised learning in the probabilistic and non-probabilistic (energy-based) frameworks, and will present several feature-learning models, including sparse coding, sparse auto-encoders, denoising auto-encoders, and Restricted Boltzmann Machines. I will also discuss supervised and semi-supervised methods for deep learning, including metric learning criteria. I will then discuss specific model architectures for image recognition, based on stacks on non-linear filter banks. A number of applications to object dectection, object recognition, and vision-based navigation for mobile robots will be described, and some will be demonstrated live.
Guillermo Sapiro, University of Minnesota
Dictionary learning for efficient signal representation
The goal of this class is to introduce participants to the area of dictionary learning for sparse representations. We will cover fundamental theory and computational algorithms as well as applications in signal processing. Topics we plan to cover include:
- Sparse coding (OMP, LASSO, group LASSO, LARS, soft thresholding, etc).
- Metric learning and k-flats.
- Dictionary learning (MOD, K-SVD, on-line learning, etc).
- Data as dictionaries and sparse graphs.
Zuowei Shen, National University of Singapore
Wavelet and Wavelet Frames in Imaging Science
From the beginning of sciences, visual observations have played major roles. With the rapid progress in video and computer technology, computers have become powerful enough to process image data. As a result, image processing techniques are now applied to virtually all natural sciences and technical disciplines.
Mathematical analysis makes image processing algorithms predictable, accurate and, in some cases, optimal. New mathematical methods often result in novel approaches that can solve previously intractable problems or that are much faster or more accurate than previous approaches. The speed up that can be gained by fast algorithm is considerable. Fast algorithms make many image processing techniques applicable and reduce the hardware cost considerably.
Wavelet and Wavelet frame based methods are relatively new mathematical tools that allow us to quickly manipulate images, for example, high-resolution image reconstructions in some applications, or image compressions in other applications. The wavelet or wavelet frame algorithms decompose and arrange an image data into strata reflecting their relative importance. This allows a rapid access to good coarse resolution of the image while retaining the flexibility for increasingly fine representations. It leads to algorithms that give sparse and accurate representations of image and medical image for efficient computation, analysis, storage, restorations and communication. In this series talk, I will illustrate how the wavelet theory is developed and applied to various applications in image processing which includes deblurring, denoising, inpainting and image decomposition.
Joseph M. Teran, UCLA
Numerical Methods for Elasticity Problems in Biomechanics
Elasticity plays a fundamental role in many biomechanics related problems. I will talk about numerical methods used for simulating elastic phenomena in soft tissues, skeletal muscles and non-Newtonian fluids. Specifically, I will discuss common difficulties encountered and my recent algorithm developments to address them. Topics include robust resolution of: severe nonlinearity, near incompressibility, extremely large deformation, collision/contact and solid/fluid coupling. I will also discuss the impact of multi-core accelerated computation for such problems and the potentially revolutionary applications it will admit.
No comments:
Post a Comment