Here is a presentation made at the CS workshop entitled Bayesian Trajectory Optimization for Magnetic Resonance Imaging Sequences by Matthias Seeger.
There is also a long list of newly found papers:
Anthony Griffin, Christos Tzagkarakis, Toni Hirvonen, Athanasios Mouchtaris and Panagiotis Tsakalides, Exploiting the Sparsity of the Sinusoidal Model Using Compressed Sensing for Audio Coding. The abstract reads:
There is also a long list of newly found papers:
Anthony Griffin, Christos Tzagkarakis, Toni Hirvonen, Athanasios Mouchtaris and Panagiotis Tsakalides, Exploiting the Sparsity of the Sinusoidal Model Using Compressed Sensing for Audio Coding. The abstract reads:
Audio signals are represented via the sinusoidal model as a summation of a small number of sinusoids. This approach introduces sparsity to the audio signals in the frequency domain, which is exploited in this paper by applying Compressed Sensing (CS) to this sparse representation. CS allows sampling of signals at a much lower rate than the Nyquist rate if they are sparse in some basis. In this manner, a novel sinusoidal audio coding approach is proposed, which differs in philosophy from current state-of-the-art methods which encode the sinusoidal parameters (amplitude, frequency, phase) directly. It is shown here that encouraging results can be obtained by this approach, although inferior at this point compared to state-of-the-art. Several practical implementation issues are discussed, such as quantization of the CS samples, frequency resolution vs. coding gain, error checking, etc., and directions for future research in this framework are proposed.
* Sparse Recovery of Positive Signals with Minimal Expansion by M. Amin Khajehnejad Alexandros Dimakis, Weiyu Xu, Babak Hassibi. The abstract reads:
We investigate the sparse recovery problem of reconstructing a high-dimensional non-negative sparse vector from lower dimensional linear measurements. While much work has focused on dense measurement matrices, sparse measurement schemes are crucial in applications, such as DNA microarrays and sensor networks, where dense measurements are not practically feasible. One possible construction uses the adjacency matrices of expander graphs, which often leads to recovery algorithms much more efficient than ℓ1 minimization. However, to date, constructions based on expanders have required very high expansion coefficients which can potentially make the construction of such graphs difficult and the size of the recoverable sets small. In this paper, we construct sparse measurement matrices for the recovery of non-negative vectors, using perturbations of the adjacency matrix of an expander graph with much smaller expansion coefficient. We present a necessary and sufficient condition for ℓ1 optimization to successfully recover the unknown vector and obtain expressions for the recovery threshold. For certain classes of measurement matrices, this necessary and sufficient condition is further equivalent to the existence of a “unique” vector in the constraint set, which opens the door to alternative algorithms to ℓ1 minimization. We further show that the minimal expansion we use is necessary for any graph for which sparse recovery is possible and that therefore our construction is tight. We finally present a novel recovery algorithm that exploits expansion and is much faster than ℓ1 optimization. Finally, we demonstrate through theoretical bounds, as well as simulation, that our method is robust to noise and approximate sparsity.
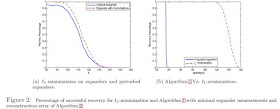
This is a must read paper. Their presentation of the main issue is crystal clear:
...It turns out that, due to the additional non-negativity constraint, one requires significantly fewer measurements to recover k-sparse non-negative signals. The non-negative case has also been studied in [5] for Gaussian matrices and also in the work of Bruckstein et al. [10], which further proposes a “matching pursuit” type of recovery algorithm. See also [29] for another example.
The success of a measurement matrix is often certified by a so-called Restricted Isometry Property (RIP) which guarantees the success of ℓ1 minimization. Recently, Berinde et al. [6] showed that the adjacency matrices of suitable unbalanced expander graphs satisfy an RIP property for ℓp1 norm. However, it turns out that RIP conditions are only sufficient and often fail to characterize all good measurement matrices. A complete characterization of good measurement matrices was recently given in terms of their null space. More precisely, as stated in previous work (e.g. [17, 20, 22, 24]), if for any vector w in the null space of A, the sum of the absolute values of any k elements of w is less that the sum of the absolute values of the rest of the elements, then the solution to min kxk0 subject toAx = y can always be obtained by solving min kxk1 subject to Ax = y, provided x is k-sparse.1 This condition is stated in the work of Donoho [1] as the k-neighborly polytope property of A, and in the work of Candes et al. as the uncertainty principle [3]. Donoho et al. also have been able to show the validity of this condition with high probability for random i.i.d Gaussian matrices and are therefore able to compute fairly tight thresholds on when linear programming- based compressed sensing works [2]. The first analysis of the null space for expander graphs has been done by Indyk [9], where it was shown that every (2k,ǫ) expander graph2 with ǫ \le 16 will have a well supported null space. See also [18] for explicit constructions using expander graphs....
The authors then go on to explain their contribution.
At hand is really the ability to produce sparse measurement matrices and associated fast reconstruction algorithms.
....We present a necessary and sufficient condition that completely characterizes the success of ℓ1-minimization for non-negative signals, similar to the null space condition for the general case. Our condition requires that all the vectors in the null space of A have sufficiently large negative support (i.e. a large number of negative entries). It further turns out that, for a certain class of measurement matrices A, this condition is nothing but the condition for the existence of a “unique” vector in the constraint set {x|Ax = y, x \ge 0}. This therefore suggests that any other convex optimization problem over this constraint set can find the solution. (We exploit this fact later to find faster alternatives to ℓ1 minimization.) We then use the necessary and sufficient characterization to construct sparse measurement matrices. Our construction relies on starting with the adjacency matrix of an unbalanced expander (with constant degree) and adding suitable small perturbations to the non-zero entries....
At hand is really the ability to produce sparse measurement matrices and associated fast reconstruction algorithms.
* Error-Correcting Tournaments by Alina Beygelzimer, John Langford, Pradeep Ravikumar. The abstract reads:
* Target Detection via Network Filtering by Shu Yang, Eric Kolaczyk. The abstract reads:We present a family of pairwise tournaments reducing $k$-class classification to binary classification. These reductions are provably robust against a constant fraction of binary errors. The results improve on the PECOC construction \cite{SECOC} with an exponential improvement in computation, from $O(k)$ to $O(\log_2 k)$, and the removal of a square root in the regret dependence, matching the best possible computation and regret up to a constant.
Could that be used to determine some knowledge in the current crisis ?A method of `network filtering' has been proposed recently to detect the effects of certain external perturbations on the interacting members in a network. However, with large networks, the goal of detection seems a priori difficult to achieve, especially since the number of observations available often is much smaller than the number of variables describing the effects of the underlying network. Under the assumption that the network possesses a certain sparsity property, we provide a formal characterization of the accuracy with which the external effects can be detected, using a network filtering system that combines Lasso regression in a sparse simultaneous equation model with simple residual analysis. We explore the implications of the technical conditions underlying our characterization, in the context of various network topologies, and we illustrate our method using simulated data.
* Uniqueness of Low-Rank Matrix Completion by Rigidity Theory by Amit Singer, Mihai Cucuringu. The abstract reads:
The problem of completing a low-rank matrix from a subset of its entries is often encountered in the analysis of incomplete data sets exhibiting an underlying factor model with applications in collaborative filtering, computer vision and control. Most recent work had been focused on constructing efficient algorithms for exact or approximate recovery of the missing matrix entries and proving lower bounds for the number of known entries that guarantee a successful recovery with high probability. A related problem from both the mathematical and algorithmic point of view is the distance geometry problem of realizing points in a Euclidean space from a given subset of their pairwise distances. Rigidity theory answers basic questions regarding the uniqueness of the realization satisfying a given partial set of distances. We observe that basic ideas and tools of rigidity theory can be adapted to determine uniqueness of low-rank matrix completion, where inner products play the role that distances play in rigidity theory. This observation leads to an efficient randomized algorithm for testing both local and global unique completion. Crucial to our analysis is a new matrix, which we call the completion matrix, that serves as the analogue of the rigidity matrix.
Multipath signal propagation is the defining characteristic of terrestrial wireless channels. Virtually all existing statistical models for wireless channels are implicitly based on the assumption of rich multipath, which can be traced back to the seminal works of Bello and Kennedy on the wide-sense stationary uncorrelated scattering model, and more recently to the i.i.d. model for multi-antenna channels proposed by Telatar, and Foschini and Gans. However, physical arguments and growing experimental evidence suggest that physical channels encountered in practice exhibit a sparse multipath structure that gets more pronounced as the signal space dimension gets large (e.g., due to large bandwidth or large number of antennas). In this paper, we formalize the notion of multipath sparsity and discuss applications of the emerging theory of compressed sensing for efficient estimation of sparse multipath channels.
Algorithms to construct/recover low-rank matrices satisfying a set of linear equality constraints have important applications in many signal processing contexts. Recently, theoretical guarantees for minimum-rank matrix recovery have been proven for nuclear norm minimization (NNM), which can be solved using standard convex optimization approaches. While nuclear norm minimization is effective, it can be computationally demanding. In this work, we explore the use of the PowerFactorization (PF) algorithm as a tool for rank-constrained matrix recovery. Empirical results indicate that incremented-rank PF is significantly more successful than NNM at recovering low-rank matrices, in addition to being faster.
Three properties of matrices: the spark, the mutual incoherence and the restricted isometry property have recently been introduced in the context of compressed sensing. We study these properties for matrices that are Kronecker products and show how these properties relate to those of the factors. For the mutual incoherence we also discuss results for sums of Kronecker products.
Thanks to The Google, finally, here are three talks that will take place in the near future (they are in the compressive sensing calendar). The first one will take place today:
1. Rice University
Speaker: Piotr Indyk
TI Visiting Professor, Rice University
Massachusetts Institute of Technology
Sketching, Streaming and Sub-linear Space Algorithms
Tuesday, March 3, 2009
3:30 PM to 4:30 PM
102 Keck Hall
Rice University
6100 Main St
Houston, Texas, USAData stream algorithms are algorithms that perform computation over streams of data using only a limited amount of space. The field has experienced a significant growth over the last decade. Data stream algorithms have found applications in many domains, including analysis of massive data sets and network monitoring. At the same time, the field has been enriched by the discovery of strong connections to other areas, such as metric embeddings, communication complexity and compressed sensing.
This talk will provide an overview of streaming algorithms and related concepts.
2. Nothwestern University
Emmanuel Candes
4:00 p.m
April 15, 2009
Ford ITW Auditorium
Emmanuel J. Candes, Ronald and Maxine Linde Professor of Applied and Computational Mathematics, California Institute of Technology
"Compressive Sensing: An Overview"
Abstract:
One of the central tenets of signal processing and data acquisition is the Shannon/Nyquist sampling theory: the number of samples needed to capture a signal is dictated by its bandwidth. This talk introduces a novel sampling or sensing theory which goes against this conventional wisdom. This theory now known as Compressed Sensing or Compressive Sampling allows the faithful recovery of signals and images from what appear to be highly incomplete sets of data, i.e. from far fewer measurements or data bits than traditional methods use. We will present the key ideas underlying this new sampling or sensing theory, and will survey some of the most important results. We will emphasize the practicality and the broad applicability of this technique, and discuss what we believe are far reaching implications; e.g. procedures for sensing and compressing data simultaneously and much faster. Finally, there are already many ongoing efforts to build a new generation of sensing devices based on compressed sensing and we will discuss remarkable recent progress in this area as well.
3. Princeton
PACM Colloquium
Topic: Compressive Optical Imaging
Presenter: Rebecca Willett, Electrical Engineering, Duke University
Date: Monday, March 9, 2009, Time: 4:00 p.m., Location: Fine Hall 214
Abstract:
Recent work in the emerging field of compressed sensing indicates that, when feasible, judicious selection of the type of image transformation induced by imaging systems may dramatically improve our ability to perform reconstruction, even when the number of measurements is small relative to the size and resolution of the final image. The basic idea of compressed sensing is that when an image is very sparse (i.e. zero-valued at most locations) or highly compressible in some basis, relatively few incoherent observations suffice to reconstruct the most significant non-zero basis coefficients. These theoretical results have profound implications for the design of new imaging systems, particularly when physical and economical limitations require that these systems be as small, mechanically robust, and inexpensive as possible.
In this talk I will describe the primary theory underlying compressed sensing and discuss some of the key mathematical challenges associated with its application to practical imaging systems. In particular, I will explore several novel imaging system designs based on compressed sensing, including compressive coded aperture and hyperspectral imagers, and examine the interplay between compressed sensing theory and the practical physical constraints which must be considered to effectively exploit this theory.
4. Technion
Time+Place: Thursday 05/03/2009 14:30 Room 337-8 Taub Bld.
Title: Compressed Sensing Meets Information Theory
Speaker: Dror Baron
Affiliation: Electrical Engineering, Technion
Host: Eli Ben-Sasson
Abstract:
Traditional signal acquisition techniques sample band-limited analogsignals above the Nyquist rate, which is related to the highest analogfrequency in the signal. Compressed sensing (CS) is based on therevelation that optimization routines can reconstruct a sparse signalfrom a small number of linear projections of the signal. Therefore,CS-based techniques can acquire and process sparse signals at muchlower rates. CS offers tremendous potential in applications such asbroadband analog-to-digital conversion, where the Nyquist rate exceedsthe state of the art.Information theory has numerous insights to offer CS; I will describeseveral investigations along these lines. First, distributedcompressed sensing (DCS) provides new distributed signal acquisitionalgorithms that exploit both intra- and inter-signal correlationstructures in multi-signal ensembles. DCS is immediately applicable insensor networks. Next, we leverage the remarkable success of graphreduction algorithms and LDPC channel codes to design low-complexityCS reconstruction algorithms.Linear measurements play a crucial role not only in compressed sensingbut in disciplines such as finance, where numerous noisy measurementsare needed to estimate various statistical characteristics. Indeed,many areas of science and engineering seek to extract information fromlinearly derived measurements in a computationally feasible manner.Advances toward a unified theory of linear measurement systems willenable us to effectively process the vast amounts of data beinggenerated in our dynamic world.
No comments:
Post a Comment