
From Houston, we have news from two people Wotao Yin and Volkan Cevher . Hurry up and download their papers and codes before Ike strikes and shuts down the whole city.
Wotao Yin lets us know of the new release of FPC_AS written by Zaiwen Wen and himself, a MATLAB solver for the L1 minimization problem, at:
Wotao Yin also lets us know that
FPC_AS is very different from the Bregman solver. It is currently faster and much more robust, especially for compressive sensing problems with solutions that have both very large and small nonzero components (i.e., the solutions have very large dynamic range). It was not designed to replace Bregman though; we are going to upgrade the Bregman solver to take advantages of the new algorithms in FPC_AS.
Volkan Cevher has finally updated his webpage and I have updated my webcrawler. Here are three important papers I was looking forward to reading and I think are important when one wants to devise applications for Compressive Sensing.
The first is devoted to developed a new recontruction algorithm in Sparse signal recovery using Markov random fields by Volkan Cevher, Marco Duarte, Chinmay Hegde, and Richard Baraniuk. The abstract reads:
Compressive Sensing (CS) combines sampling and compression into a single sub-Nyquist linear measurement process for sparse and compressible signals. In this paper, we extend the theory of CS to include signals that are concisely represented in terms of a graphical model. In particular, we use Markov Random Fields (MRFs) to represent sparse signals whose nonzero coefficients are clustered. Our new model-based reconstruction algorithm, dubbed Lattice Matching Pursuit (LaMP), stably recovers MRF-modeled signals using many fewer measurements and computations than the current state-of-the-art algorithms.
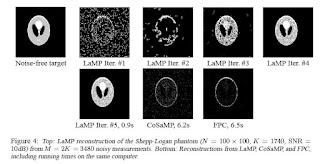
LaMP requires far fewer measurements and fewer computations for robust signal reconstruction than state-of-the-art greedy and optimization techniques.
The GCOptimization package of Olga Veksler is used in the implementation of the LaMP algorithm developed in the paper. LaMP is compared very advantageously to both CoSAMP and FPC both state of the art greedy and optimization reconstruction algorithms as can be seen in the figures.
Calibration as a sparsity problem, this is intriguing and treated in Compressive sensing for sensor calibration by Volkan Cevher, and Richard Baraniuk. The abstract reads:
We consider a calibration problem, where we determine an unknown sensor location using the known track of a calibration target and a known reference sensor location. We cast the calibration problem as a sparse approximation problem where the unknown sensor location is determined over a discrete spatial grid with respect to the reference sensor. To achieve the calibration objective, low dimensional random projections of the sensor data are passed to the reference sensor, which significantly reduces the inter-sensor communication bandwidth. The unknown sensor location is then determined by solving an ℓ1-norm minimization problem (linear program). Field data results are provided to demonstrate the effectiveness of the approach.

Finally, in what looks like an extension of a previous paper ( Compressive sensing for background subtraction ), Dikpal Reddy, Aswin Sankaranarayanan, Volkan Cevher, and Rama Chellappa expanded their work in Compressed sensing for multi-view tracking and 3-D voxel reconstruction. The abtract reads:
Compressed sensing(CS) suggests that a signal, sparse in some basis, can be recovered from a small number of random projections. In this paper, we apply the CS theory on sparse background-subtracted silhouettes and show the usefulness of such an approach in various multi-view estimation problems. The sparsity of the silhouette images corresponds to sparsity of object parameters (location, volume etc.) in the scene. We use random projections (compressed measurements) of the silhouette images for directly recovering object parameters in the scene coordinates. To keep the computational requirements of this recovery procedure reasonable, we tessellate the scene into a bunch of non-overlapping lines and perform estimation on each of these lines. Our method is scalable in the number of cameras and utilizes very few measurements for transmission among cameras. We illustrate the usefulness of our approach for multi-view tracking and 3-D voxel reconstruction problems.
Many other papers by Volkan can be found here.
No comments:
Post a Comment