Since the last Nuit Blanche in Review (June 2017), it was found that Titan had interesting chemistry. On Nuit Blanche, on the other hand, we had four implementations released by their authors, several interesting in-depth articles (some of them related to SGD and Hardware) . We had several slides and videos of meetings and schools and three job offering. Enjoy !
Implementations
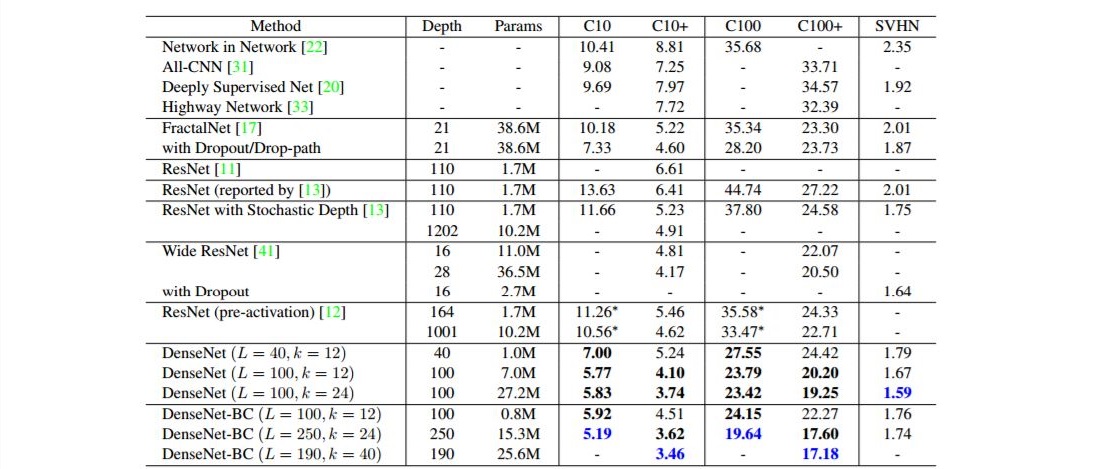
- Densely Connected Convolutional Networks - implementations -
- Localization of Sound Sources in a Room with One Microphone - implementation -
- RLAGPU: High-performance Out-of-Core Randomized Singular Value Decomposition on GPU - implementation -
- YellowFin: An automatic tuner for momentum SGD - implementation -
In-depth
SGD related
- On Unlimited Sampling
- Beyond Filters: Compact Feature Map for Portable Deep Model
- A Randomized Rounding Algorithm for Sparse PCA
- Unbiased estimates for linear regression via volume sampling
- Beyond Moore-Penrose Part II: The Sparse Pseudoinverse
SGD related
- SGD, What Is It Good For ?
- Understanding and Optimizing Asynchronous Low-Precision Stochastic Gradient Descent
- YellowFin: An automatic tuner for momentum SGD - implementation -
CS/ML Hardware
Slides
Videos
Other
Credit: Northern Summer on Titan, NASA/JPL-Caltech/Space Science Institute
Join the CompressiveSensing subreddit or the Google+ Community or the Facebook page and post there !
 Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.
Liked this entry ? subscribe to Nuit Blanche's feed, there's more where that came from. You can also subscribe to Nuit Blanche by Email, explore the Big Picture in Compressive Sensing or the Matrix Factorization Jungle and join the conversations on compressive sensing, advanced matrix factorization and calibration issues on Linkedin.
- Randomized apertures: high resolution imaging in far field
- Object classification through scattering media with deep learning on time resolved measurement
- Cardiologist-Level Arrhythmia Detection with Convolutional Neural Networks
Slides
- Slides: Deep Learning and Reinforcement Learning Summer School 2017 @ MILA Montreal, Canada
- Slides: BioComp Summer School 2017 on bio-inspired computing hardware
Videos
- Videos: DALI 2017 Symposium
- Videos: DALI 2017 - Workshop - Theory of Generative Adversarial Networks
- DALI 2017 - Workshop - Data Efficient Reinforcement Learning
- Saturday Morning Video: Martin Arjovsky (WGAN) Interview on Alex Lamb's "The Nutty Netter" YouTube channel.