Hi Igor, Since you seem to be blogging about phase-retrieval lately, your readers may be interested in our GAMP approach from Allerton 2012: http://www2.ece.ohio-state. edu/~schniter/pdf/all12_phase. Note that tables III-IV suggest that PR-GAMP has a much better phase transition than CPRL. we used the CVX implementation of CPRL that was available at the time we wrote the paper. Because it was slow, our experiments with CPRL were very limited. I plan to try the new ADMM implementation soon. As for the theory of sparse phase-retrieval, your readers may be interest in the recent work http://arxiv.org/abs/1209.4785 . cheers, Phil
Thanks Phil
The paper is: Compressive Phase Retrieval via Generalized Approximate Message Passing by Philip Schniter and Sundeep Rangan. The abstarct reads:
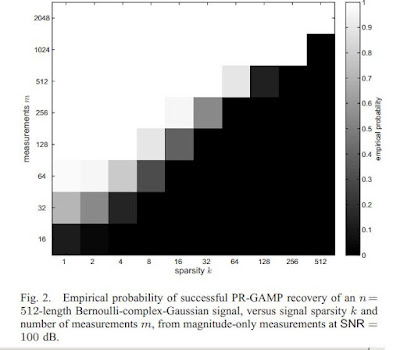
In this paper, we propose a novel approach to compressive phase retrieval based on loopy belief propagation and, in particular, on the generalized approximate message passing (GAMP) algorithm. Numerical results show that the proposed PR-GAMP algorithm has excellent phase-transition behavior, noise robustness, and runtime. In particular, for successful recovery of synthetic Bernoulli-circular-Gaussian signals, PRGAMP requires ≈ 4 times the number of measurements as a phase-oracle version of GAMP and, at moderate to large SNR, the NMSE of PR-GAMP is only ≈ 3 dB worse than that of phase-oracle GAMP. A comparison to the recently proposed convex-relation approach known as “CPRL” reveals PR-GAMP’s superior phase transition and orders-of-magnitude faster runtimes, especially as the problem dimensions increase. When applied to the recovery of a 65k-pixel grayscale image from 32k randomly masked magnitude measurements, numerical results show a median PR-GAMP runtime of only 13.4 seconds.
The other theory paper I missed is: Sparse Signal Recovery from Quadratic Measurements via Convex Programming by Xiaodong Li, Vladislav Voroninski. The abstract reads:
In this paper we consider a system of quadratic equations |z_j, x|^2 = b_j, j = 1, ..., m, where x in R^n is unknown while normal random vectors z_j in R_n and quadratic measurements b_j in R are known. The system is assumed to be underdetermined, i.e., m \lt n. We prove that if there exists a sparse solution x, i.e., at most k components of x are non-zero, then by solving a convex optimization program, we can solve for x up to a multiplicative constant with high probability, provided that k \le O((m/log n)^(1/2)). On the other hand, we prove that k <= O(log n (m)^(1/2)) is necessary for a class of naive convex relaxations to be exact.
No comments:
Post a Comment