On the Local Correctness of L^1 Minimization for Dictionary Learning, A Panorama on Multiscale Geometric Representations, Intertwining Spatial, Directional and Frequency Selectivity

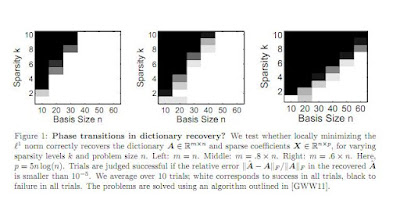
At the SMALL meeting, there was a presentation by John Wright, ( here is the video and the attendant presentation ), today we have the attendant paper: On the Local Correctness of L^1 Minimization for Dictionary Learning by Quan Geng, Huan Wang, John Wright. The abstract reads:

The idea that many important classes of signals can be well-represented by linear combinations of a small set of atoms selected from a given dictionary has had dramatic impact on the theory and practice of signal processing. For practical problems in which an appropriate sparsifying dictionary is not known ahead of time, a very popular and successful heuristic is to search for a dictionary that minimizes an appropriate sparsity surrogate over a given set of sample data. While this idea is appealing, the behavior of these algorithms is largely a mystery; although there is a body of empirical evidence suggesting they do learn very effective representations, there is little theory to guarantee when they will behave correctly, or when the learned dictionary can be expected to generalize. In this paper, we take a step towards such a theory. We show that under mild hypotheses, the dictionary learning problem is locally well-posed: the desired solution is indeed a local minimum of the $\ell^1$ norm. Namely, if $\mb A \in \Re^{m \times n}$ is an incoherent (and possibly overcomplete) dictionary, and the coefficients $\mb X \in \Re^{n \times p}$ follow a random sparse model, then with high probability $(\mb A,\mb X)$ is a local minimum of the $\ell^1$ norm over the manifold of factorizations $(\mb A',\mb X')$ satisfying $\mb A' \mb X' = \mb Y$, provided the number of samples $p = \Omega(n^3 k)$. For overcomplete $\mb A$, this is the first result showing that the dictionary learning problem is locally solvable. Our analysis draws on tools developed for the problem of completing a low-rank matrix from a small subset of its entries, which allow us to overcome a number of technical obstacles; in particular, the absence of the restricted isometry property.

This is a very interesting paper. An eloquent introduction states:

This idea has several appeals: Given the recent proliferation of new and exotic types of data (images, videos, web and bioinformatic data, ect.), it may not be possible to invest the intellectual e ort required to develop optimal representations for each new class of signal we encounter. At the same time, data are becoming increasingly high-dimensional, a fact which stretches the limitations of our human intuition, potentially limiting our ability to develop e ective data representations. It may be possible for an automatic procedure to discover useful structure in the data that is not readily apparent to us.

so we are getting closer to Skynet :). Anyway, I note that once more the work of David Gross has helped a lot once more and that this work has a direct impact on calibration type of exercises.

On a different note, here is a paper on dictionaries we have built in the past few years based on our intuition:; A Panorama on Multiscale Geometric Representations, Intertwining Spatial, Directional and Frequency Selectivity by Laurent Jacques, Laurent Duval, Caroline Chaux, Gabriel Peyré. The abstract reads:

The richness of natural images makes the quest for optimal representations in image processing and computer vision challenging. This fact has not prevented the design of candidates, convenient for rendering smooth regions, contours and textures at the same time, with compromises between efficiency and complexity. The most recent ones, proposed in the past decade, share an hybrid heritage highlighting the multiscale and oriented nature of edges and patterns in images. This paper endeavors a panorama of the aforementioned literature on decompositions in multiscale, multi-orientation bases or dictionaries. They typically exhibit redundancy to improve both the sparsity of the representation, and sometimes its invariance to various geometric deformations. Oriented multiscale dictionaries extend traditional wavelet processing and may offer rotation invariance. Highly redundant dictionaries require specific algorithms to simplify the search for an efficient (sparse) representation. We also discuss the extension of multiscale geometric decompositions to non-Euclidean domains such as the sphere $S^2$ and arbitrary meshed surfaces in $\Rbb^3$. The apt and patented etymology of panorama suggests an overview based on a choice of overlapping "pictures", i.e., selected from a broad set of computationally efficient mathematical tools. We hope this work help enlighten a substantial fraction of the present exciting research in image understanding, targeted to better capture data diversity.